GoodCoder666的个人博客

Mathematica 入门

2024-01-25 · 11 min read

Mathematica & Wolfram Language

前言

Wolfram Mathematica（简称 MMA），是由 Wolfram Research 开发的科学计算软件。本文我们将介绍 Mathematica 的界面、语法和基本应用。类似的软件还有 MATLAB 和 Maple 等。

MMA 官网：https://www.wolfram.com/mathematica/

MMA 的安装及激活：Mathematica安装激活极简教程 - 科研小飞 (知乎)

本文适合有一定编程基础的读者。当然，如果你不了解编程也没关系，直接跳过相关部分即可。屏幕截图全部来自 Windows 11，Mathematica 13.3。（最新版本 14.0 已经在 2023 年 12 月发布，语法向下兼容）

演示使用的 MMA 版本

1. 界面

安装并正确激活 MMA 后，新建笔记本，应该能看到如下的界面：

一张图带你快速熟悉 MMA 的界面：

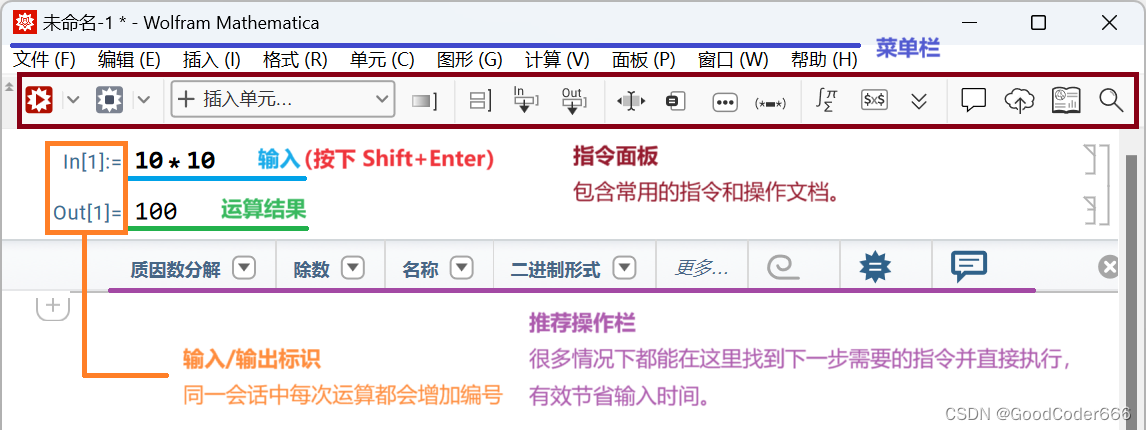
几个需要注意的点：

Enter 默认换行，执行代码需要用 Shift+Enter。
指令面板左侧的红三角形也可执行代码，灰色的正方形用于终止正在进行的运算。
MMA 带有 Notebook（笔记本）功能，由于其主要用于计算而不是笔记，本文不详细介绍，若需要使用可自行查阅相关资料。

对于任意输入或输出，按下Ctrl+Shift+I即可显示输入（代码）形式，按下Ctrl+Shift+N即可显示数学形式。后面会对两种显示形式进行详细讲解。

2. 语法

Mathematica 实质是一个 Wolfram Language 的解释器，所以使用它之前必须学习 WL 的语法。
这里介绍基本语法和常用的指令。

2.1 帮助文档

首先来了解帮助文档的使用。输入 ? Solve 来获取 Solve 函数的说明：

? 后面可以跟任何函数名，MMA 会直接在笔记本中输出简化版的帮助文档。可以选择输出右上角的 i 来获取更详细的文档（优先打开离线文档，不存在则默认打开在线文档）。菜单栏中的 “帮助 -> Wolfram 参考资料” 可以打开完整版文档。

2.2 注释

(* 注释 *)

如上，MMA 的注释使用 (* 和 *) 来标注，用法类似于 C/C++ 中的 /* 和 */。注释可以添加在代码的任何位置，它们会被自动忽略。例如：

1 + 1 (*Hello*)
1 + (*World*)1

这两行代码在实际执行中与 1 + 1 无区别：

2.3 括号

在学习 MMA 的函数之前，一定要先学会括号的使用！！
官方参考文档：正确使用括号和大括号

MMA 中共有四种括号，分别为 ()、[]、{} 和 [[]]，具体作用如下：

圆括号 `()`

用作对表达式编组和确定运算的优先次序：

方括号 `[]`

表示函数的调用和传参：

大括号 `{}`

表示列表：

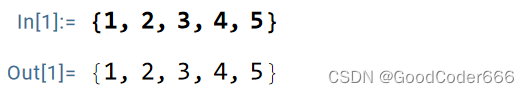
列表的具体使用后续会介绍。

双方括号 `[[]]`

表示对列表元素的访问，实质是函数 Part 的简写形式：

同样会在后面具体介绍。

2.4 运算与表达式

MMA 支持基本的数学运算，见下表：

名称	符号形式	函数形式	数学形式
加法	`a + b`	`Plus[a, b]`	$a+b$
减法	`a - b`	`Subtract[a, b]`	$a-b$
乘法	`a * b`^[1]	`Times[a, b]`	$a\times b$
除法	`a / b`	`Divide[a, b]`	$\frac ab$
幂	`a ^ b`	`Power[a, b]`	$a^b$
模余	-	`Mod[a, b]`	$a\bmod b$

数字和符号都可以参与运算：

表达式是一个或多个运算/函数调用的组合，使用()指定优先级。上图中 4*5、a+a、3 x y/y 都是合法的表达式。

需要注意的是，MMA 只会对输入的表达式进行约分、合并同类项，而不会自动执行需要展开的化简。必要时可以使用 Simplify 或 FullSimplify 函数：

关于函数的使用，后面会详解。

布尔表达式

表达式也可以是等式或不等式：

注意等式用两个等号 == 连接，单个等号表示变量赋值。
不等式可以用 !=（不等于）、>（大于）、>=（大于等于）、<（小于）、<=（小于等于）连接。!=、>= 和 <= 在输入时会自动转换为相应的数学符号。

这类返回值为 True（真）或 False（假）的表达式，我们统称为布尔表达式。可以用 && 和 || 运算符来连接两个布尔表达式，分别表示“与”“或”，所得结果仍为布尔表达式。

绝大部分布尔表达式都不能自动化简，但可以通过 Simplify、FullSimplify 或 Solve、Reduce 来化简或求解：

2.5 变量与常数

MMA 中，使用 变量名 = 值 的形式来声明或赋值变量：

由上方 10a + 3 的计算结果可知，表达式中所有已声明的变量都会被替换成变量值。变量的声明也可以包含其他变量和符号，此时仍符合变量替换法则：

用于解方程的 Solve 函数没有返回 $a$ 的解，而是返回 $x$ 的解，说明表达式在解析时 $a$ 被自动替换为了 $x$ 。

除此之外，还可以用类似于 Python 的语法，同时赋值多个变量：
{a, b, c} = {1, 2, 3}
这行代码可以把变量 $a,b,c$ 分别赋值为 $1,2,3$ 。

若要取消声明一个变量，可以使用 Clear[变量名]：

在使用 MMA 的过程中，我们会发现某些特定符号不能声明为变量，且有一个固定不变的值。这些是内置常量：

常量	名称	近似值	数学形式
`Pi`	圆周率	$3.141592654$	$\pi$
`E`	自然常数	$2.718281828$	$\mathrm e$
`I`	虚数单位	-	$i$
`Infinity`	无穷大	-	$\infty$
`Degree`	度	-	$\degree$

2.6 函数

在前面的讲解中，我们多次提到函数。现在，让我们详细解读函数的使用。

调用

要调用一个函数，只需输入 函数名[参数1, 参数2, ...] 即可：

对于只有一个参数的函数，可以用 参数 // 函数名 的形式调用。这种形式常用于 Simplify（化简）、FullSimplify（完全简化）和 N（数值运算）的调用：

这种写法的最大优点在于可以链式调用：

定义

说完了函数的调用，再来说说新函数的定义。

MMA 中，定义新函数的语法为 函数名[参数1_, 参数2_, ...] := 返回值。注意每个参数名后面都要加一个下划线（_）。

定义新函数推荐用 :=，但使用 = 也可行。

拓展 - 定义递归函数
参考下面定义斐波那契数列的格式：

3. 内置函数

MMA 中有将近 $6000$ 个内置函数^[2]，它们都以大写字母开头。下面介绍几种常用的内置函数：

3.1 数值运算 N

数值运算函数 N：

N[expr] 给出 $\mathrm{expr}$ 的数值值
N[expr, n] 尝试给出具有 $n$ 位精度的结果

使用示例：

3.2 三角函数

MMA 内置了各类三角函数，它们全部使用习惯名称且首字母大写（Sin、Sinh、ArcSin），这里不一一阐释。
只说一个注意点，MMA 中三角函数的参数默认是弧度，若要使用角度必须加上 Degree 单位：

3.3 解方程和不等式 Solve/Reduce

解方程 Solve：

解不等式用 Reduce：

Reduce 还有更高级的使用，可以约化各种表达式：

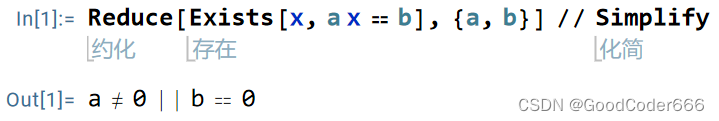
这句话说的是：求解 $a,b$ 的范围，使得存在 $x$ 满足等式 $ax=b$ 。实际上就是在求解使一元一次方程有解的参数值。注意 Solve 和 Reduce 不一定总返回最简形式的表达式，很多情况下需要手动调用 Simplify 或 FullSimplify 进行化简。感兴趣的读者可以自行测试上面的例子中不使用 Simplify 的返回结果。

3.4 解方程的其他方法 NSolve/FindInstance

NSolve 用法同 Solve，但会返回数值解而不是精确解。相当于 Solve[...] // N。
FindInstance 用法同 Solve，但添加了一个参数表示至多返回解的个数（默认为 $1$ ）：

3.5 极点值 Maximize/Minimize

Minimize 返回函数（在限制条件下）的最小值以及取到最小值的（一种）变量值：

如上图中的示例，Minimize 支持多个变量，可以指定条件，也可指定求解域。
Maximize 用法完全相同，返回最大值，此处略过。

3.6 偏导 D

偏导 D 的两种最常用用法：

D[f, x] 给出 $f$ 关于 $x$ 的偏导。
D[f, {x, n}] 给出 $f$ 关于 $x$ 的 $n$ 阶偏导。

示例略。注意 f'[x] 可以直接求出 f[x] 的导数：

3.7 积分 Integrate

积分 Integrate：

Integrate[f, x] 给出不定积分 $\int f~\mathrm{d}x$ 。
Integrate[f, {x, x_min, x_max}] 给出定积分 $\int_{x_{min}}^{x_{max}} f~\mathrm{d}x$ 。
Integrate[f, {x, x_min, x_max}, {y, y_min, y_max}, ...] 给出多重积分 $\int_{x_{min}}^{x_{max}} \mathrm{d}x \int_{y_{min}}^{y_{max}} \mathrm{d}y\dots f$ 。

一个简单的定积分示例：

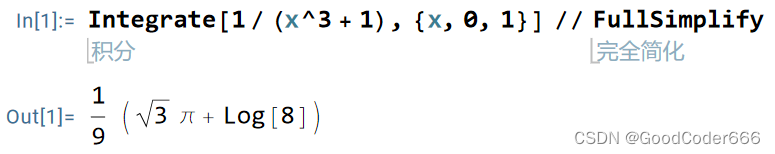
3.8 展开 Expand/ExpandAll

Expand 很好理解，Expand[expr] 会展开表达式 $\mathrm{expr}$ 中的乘积和正整数幂。限于篇幅，这里不提供使用范例，可参考官方文档。
ExpandAll 在 Expand 的基础上，会展开表达式中任意位置的乘积和整数幂。如表达式 Sin[(1 + x)^3]，Expand 不会展开其中的 (1+x)^3，而 ExpandAll 会。

3.9 因式分解 Factor

Factor[poly]：在整数上对一个多项式分解因式。使用示例参考官方文档。

3.10 绘图 Plot/Plot3D

Plot 和 Plot3D 的用法较为复杂，这里只介绍最基本的函数绘图：

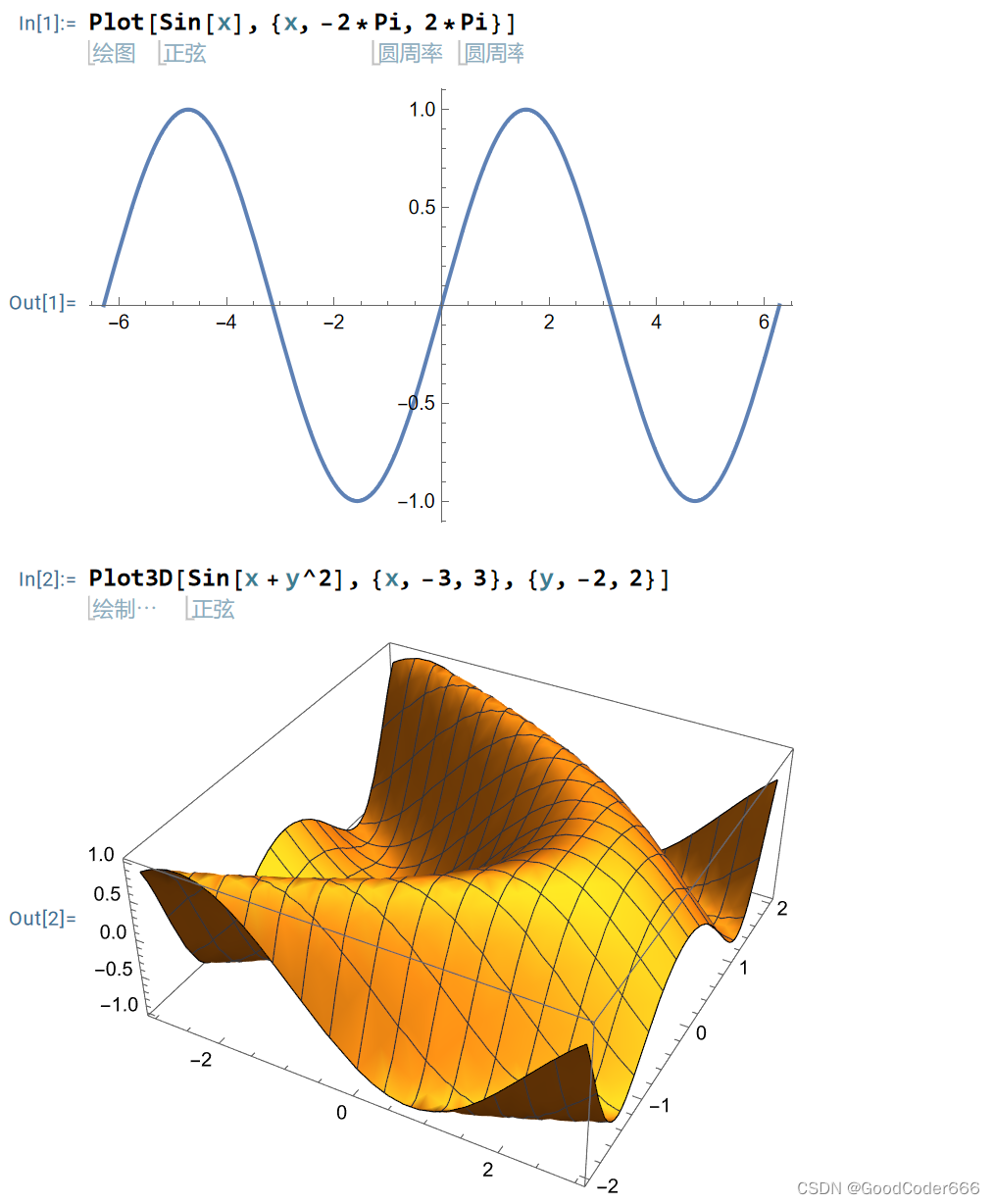
两个语句分别绘制：

$\sin(x)$ 的图像，其中 $-2\pi\le x\le 2\pi$ ；
$\sin(x+y^2)$ 的图像，其中 $-3\le x\le 3$ ， $-2\le y\le 2$ 。

4. 总结

我自己当初学习 MMA 时，被网上杂乱的教程搞得混乱不堪。因此就想写一篇教程，涵盖所有常用语法知识点，并让初学者避开我自己踩的一些坑。
初衷是写个简明的教程，结果一写就是八千多字…… 也感谢认真读到这里的读者们！
后续可能还会更一些用 Mathematica 解决数学和实际问题的文章，敬请期待！

乘法也可简写为 a b（中间必须有空格）。MMA 中，大部分空格可省略，但是乘法的空格不能省略（若写作没有空格的 ab 会被认为是一个变量）。 ↩︎
https://www.wolfram.com/language/fast-introduction-for-programmers/en/built-in-functions/ ↩︎