前言
如题,这是我的一个探索型项目。其目的并不是为了达成什么效果,而是在尝试的过程中学习知识。本文包含简要的技术报告,亦有过程中的一些心得体会。评论系统还没弄好,若有任何想法或疑问欢迎直接在项目的 Issue / Discussion 中发出来。
最近在研究强化学习(RL),其中特别喜欢 AlphaZero 算法。它是 2016 年击败世界围棋冠军李世石的 AlphaGo 演化而来的通用强化学习算法。一些主流的强化学习介绍书籍一般止步于 PPO、SAC 或 DDPG 等方法(而没有 AlphaZero、MuZero 系列),私以为是一个很大的错误。
从根源上来看,AlphaZero 属于 Model-Based RL 的范畴,这与以 Q-learning、Actor-Critic 为代表的 Model-Free RL 有本质区别。其在于使用了环境模型(游戏模拟器)进行树搜索推演最优策略,而不是通过大量试错来逐步提升预期收益。良好的环境模型对于这类算法的结果至关重要;在棋类游戏中,明确的规则直接给出了一个完美的环境模型。而真实物理世界中的环境十分复杂,难以用简单的规则去描述,这成为了阻碍强化学习技术落地应用的关键瓶颈。Meta 近期开源的 V-JEPA 2 就是构建世界模型的重要一步,非常建议大家去进一步了解。
受计算资源的限制,我选择了 Saiblo 四子棋 作为游戏环境 1,状态空间相对较小,但也有一定的复杂性,没有已知必胜策略。另外平台上也有非常优秀的传统方法用于比较,可以获得一个相对客观的算法棋力评测。在此非常感谢清华大学提供的平台,在满足校内同学实验需求的同时能给校外的爱好者带来很大便利。
由于我的 AI 使用了 KataGo 中的一些算法改进,故命名为 katac4,代码在 GitHub 上完全开源。
截至文章写作时间(2025.06.27),katac4 在游戏天梯上以遥遥领先的分数稳居榜一:
AlphaZero 速览
网上通俗易懂地介绍 AlphaZero 的文章不在少数,因此这里仅作较为抽象的简要概述(思路参考 KataGo 论文)。
算法通过神经网络引导的蒙特卡洛树搜索(MCTS)进行自我对弈以生成训练数据。搜索过程即反复扩展游戏树:每次从根节点出发沿一条链走到叶子节点,在节点 $n$ 处选择使以下式子最大的子节点 $c$ 进行访问:
$$ \mathrm{PUCT}(c)=V(c)+c_\mathrm{PUCT}P(c) \frac{\sqrt{\sum_{c'}N(c')}}{1+N(c)} $$其中 $V(c)$ 是 $c$ 子树中所有节点的平均预测效用值,$P(c)$ 是神经网络给出的 $c$ 对应动作先验概率,$N(c)$ 为之前通过节点 $c$ 进行模拟的次数,常数 $c_\mathrm{PUCT}=1.1$;$c'$ 表示 $n$ 的所有子节点。
不同于 $\epsilon$-greedy 算法,AlphaZero 通过对根节点处的先验概率施加 Dirichlet 噪声以增强探索:
$$ P(c)=0.75P_{\text{raw}}(c)+0.25\eta $$其中 $\eta$ 采样自参数 $\alpha=0.8$ 的 Dirichlet 分布,$P_{\text{raw}}$ 表示神经网络给出的原始策略分布。
设搜索树的根有 $k$ 个子节点 $u_1,\dots,u_k$,它们对应的动作分别为 $a_1,\dots,a_k$。则 MCTS 的 visit distribution 正比于 $N(u_i)$:
$$ \pi(a_k|s_t)=\frac{N(u_k)}{\sum_{i=1}^k N(u_i)} $$这是神经网络的训练目标,同时用于选择自对弈时的下一个动作(以动态变化的温度 $T$ 采样)。自对弈的起点为初始局面。在推理(实战)阶段,一般直接选择该分布中概率最大的动作,也就是访问次数最多的。
神经网络接受当前的局面状态 $s_t$ 作为输入,预测下一个动作的概率分布 $\pi$ 和局面胜率 $z$。其损失函数为:
$$ L=-c_g \sum_r z(r) \log(\hat z(r))-\sum_m \pi(m) \log(\hat \pi(m))+c_{L2} ||\boldsymbol\theta||^2 $$其中 $r \in \{\text{win}, \text{loss}, \text{draw}\}$ 表示当前玩家视角下的游戏结果,常数 $c_g=1.5,c_{L2}=3\times 10^{-5}$。整个损失函数即为以下三部分的加权和:
- 胜率预测与实际结果的 Cross Entropy 2;
- 策略分布预测与 MCTS visit distribution 的 Soft Cross Entropy;
- 对神经网络参数 $\boldsymbol\theta$ 的 L2 正则化。
策略更新采用 Off-policy 的方式,维护经验回放池(replay buffer),每轮自对弈完成后将新的经验数据加入回放池,再从中采样一个大小为 $B$ 的小批量进行梯度下降更新。使用 SGD with Momentum 优化器,学习率随训练阶段调整。
整体上,AlphaZero 与策略迭代算法的核心思想是一致的,只是用 MCTS 同时完成了策略评估和策略提升的任务。
训练,退火
退火的思想对于成功训练一个 AlphaZero Agent 至关重要。这里涉及到非常多的细节,建议大家参考代码,我在此列出几个关键要点:
- 从 visit distribution 中采样动作的温度 $T=0.8^{1+step/boardsize}$。AlphaZero_Gomoku 中使用常数 $T=1$,实践证明这是完全错误的。在一盘棋后期很容易”一招不慎,满盘皆输“,若直接根据 visit distribution 采样动作会产生大量错误 game outcome 样本,导致整个训练崩溃。
- 神经网络给出的策略,在根节点应用温度 $T=\max(1.03,1.35\times0.66^{step/boardsize})$。这可以确保一定的探索性,增强训练稳定性。
- 学习率退火。训练的前期($5\%$ 迭代次数)使用 $1/3$ 的正常学习率(防止前期训练大幅波动),$72\%$ 以后使用 $1/10$ 的正常学习率(最大化提升棋力)。
很多超参数不一定最优,都是随手设置的,但是它们的组合确实有效,希望能给大家提供一些参考价值。
算法优化
Recomputing the AlphaGo Zero weights will take about 1700 years on commodity hardware.
这句话来自 Leela Zero 项目的 README 文档。AlphaZero 本身的探索过程十分低效,但是利用精心设计的算法优化可以显著缩短其训练周期。KataGo 论文中的方法共同作用,可将训练效率提升 ~50x。下面介绍我使用的一些算法优化,其中部分来自 KataGo。
梯度累加
我们的游戏环境——Saiblo 四子棋的棋盘大小不固定,长宽均在 $[9,12]$ 区间内取值。因此共有 $16$ 种不同大小的棋盘。
为了适应不同的棋盘大小,做以下两点改进:
- 神经网络采用全卷积(FCN)架构3,策略头输出与输入状态大小保持一致。
- 从 replay buffer 中采样时,由直接采样 $256$ 个样本改为每种棋盘大小各采样 $16$ 个样本。对不同棋盘大小的样本各进行一次 forward pass,计算梯度并累加。然后正常 backward + step 即可。
KataGo 中采用的是 board masking 的方式适应不同输入,而这涉及到繁琐的细节实现。直接采用最简单的梯度累加来完成这一点,虽效率稍低但方便了许多。
动作空间剪枝
这个方法的动机非常简单:人工筛选掉可以被证明严格错误的着法,将其视为不合法动作,排除出 MCTS 计算。
实现只需非常小的代码更改,总结为两条规律:
- 我走一步棋直接赢,则必走;
- 对手走一步棋直接赢,则我必堵。
这种优化非常简单,却能显著加快训练前期探索,让模型迅速理解游戏规则。同时,这也能避免一些很糟糕的盲点,尤其是对手在棋盘边缘成三有可能会被 CNN 忽视。
First Play Urgency (FPU)
这项优化源自 Leela Zero。
细心的读者肯定会问:PUCT 计算时,若子节点没有访问即 $N(c)=0$,$V(c)$ 怎么定义?
AlphaGo Zero 给出了标准答案:$V(c)=0$。但 Leela Zero 社区讨论发现,这并不是最优选择。他们选择:
$$ V(c)=V(n)-c_\text{FPU}\sqrt{P_\text{explored}} $$其中 $n$ 为父亲节点,常数 $c_\text{FPU}=0.2$,$P_\text{explored}$ 为访问过至少一次的子节点的策略先验概率总和:
$$ P_\text{explored}=\sum_{c'|N(c')>0} P(c') $$读者可以自行思考这种做法的合理性。Lc0 的一个讨论指出,对于实力较强的神经网络,此法足以带来 ~200 Elo 的提升。
模拟上限随机化
对应 KataGo 论文中的 Playout Cap Randomization。
AlphaZero 中的两个输出头训练所需 playouts 并不相同。一些非正式研究表明,训练 policy head 最高效的模拟次数设置与 AlphaZero 的 $N=800$ 十分接近,但在 AlphaGo 的第一个版本中只用 $N=1$ 也能训练出较好的 value head。为了缓解二者的紧张关系,我们取一个较小的模拟次数 $n < N$,并以概率 $p$ 执行 fast search($n$ 次模拟),其余情况正常 full search($N$ 次模拟)。fast search 产生的样本不用于策略训练4。
我的超参数选择是 $(N,n)=(800,160)$,以及 $p=0.25$。个人感觉对于四子棋这种游戏,模拟次数再小一点应该也没事。
强制探索 & 策略剪枝
对应 KataGo 论文中的 Forced Playouts and Policy Target Pruning。
前面提到,为了增强探索,AlphaZero 在根节点处引入 Dirichlet noise。然而这种方式并不能保证好的着法一定能被发现。
设想下面这个场景:
- 游戏状态 $s_t$。当前的神经网络十分青睐着法 $a$,而实际最优着法为 $a^*$。在输出的策略分布中,$a$ 获得了高于 $80\%$ 的概率,$a^*$ 不到 $5\%$。
- 引入 Dirichlet noise。$a$ 的概率仍然很大,$a^*$ 被“选中”来到 $10\%$。假设此时 $P(a)$ 正好为 $80\%$。
- MCTS 依次访问 $a$ 和 $a^*$。此时,价值网络仍不看好 $a^*$ 走到的状态 $s^*$,还是倾向于 $a$ 走到的状态 $s$,给出 $V(s^*)=-0.8$ 和 $V(s)=-0.1$。
- 现在的总模拟次数 $N=2$。根据 PUCT 公式可知 $\text{PUCT}(a)=0.34,\text{PUCT}(a^*)=-0.745$。这时二者 PUCT 值已经差距巨大,若 MCTS 不断选择 $a$ 进行访问并保持 $V(s)$ 不变,要到将近 $200$ 次模拟的时候才会使 $\text{PUCT}(a^*)\ge\text{PUCT}(a)$,此时 $1/4$ 的模拟次数已经被浪费了;并且如果 $a^*$ 再一次被给予差评,又要等上很长一段时间才能获得下一次访问。
由此可见,即使 Dirichlet noise 运气很好落在了正确的着法上,策略和价值网络共同的盲点仍然可能未被正确处理。故引入强制探索(Forced Playouts)机制,确保根节点的每个孩子都获得至少 $\lceil n_\text{forced} \rceil$ 次访问:
$$ n_\text{forced}(c)=\left(kP(c)\sum_{c'}N(c')\right)^{1/2} $$
沿用 KataGo 的设置,常数 $k=2$。
与此同时,为了消去 Dirichlet noise 和 Forced Playouts 共同带来的大量噪声,我们在 MCTS 完成后对 visit distribution 进行策略剪枝:
- 找到访问次数 $N(c)$ 最多的孩子 $c^*$。
- 对于其他子节点 $c$,减去尽可能多的访问次数,确保 $\text{PUCT}(a^*) > \text{PUCT}(a)$ 且减掉的次数不超过 $n_\text{forced}(c)$。
我这里选择直接使用不等式解出剪枝后的访问次数:
$$ N'(c)=\mathrm{clip}\left(\left\lceil\frac{P\sqrt N}{V+\text{PUCT}(c^*)}-1\right\rceil,N-n_\text{forced},N\right) $$为了方便阅读,以上公式中直接用 $N$ 指代 $N(c)$,$P$ 指代 $P(c)$,etc.
以下使用/不使用策略剪枝的效果对比来自 KataGo 论文。黑:$p \approx 2\times 10^{-4}$;绿: $p \approx 1$。
 |
 |
|---|---|
| 使用策略剪枝 | 不使用策略剪枝 |
动态经验回放池
来自 KataGo 论文中 Appendix C: Training Details。
Off-policy 的强化学习算法中,经验回放池的大小(容纳样本数)大多是固定的,常设置在 $[2^{14},2^{20}]$ 区间内。而我们采取一种亚线性的增长策略:
$$ N_{\text{window}} = c \left( 1 + \beta \frac{ ( N_{\text{total}} / c ) ^ \alpha - 1} { \alpha } \right) $$其中 $N_{\text{total}} $ 为当前训练过程生成的样本总数,$c=250000,\alpha=0.75,\beta=0.4$。这实际上就是对 $f(n)=n^\alpha$ 应用线性变换,使得 $f(c)=c$ 且 $f'(c)=\beta$。这样就能快速舍弃前期产生的低质量着法,并在后期增加训练样本多样性,有效抑制过拟合。
蒙特卡洛图搜索(MCGS)
见 KataGo/docs/GraphSearch.md。非常感谢 David Wu 提供的通俗易懂的讲解;我在做这个项目过程中还发现了其中一处 typo 并 PR 修复了 😆
整体思路:
-
对局面实现 Zobrist hash,扩展叶子时优先从哈希表中查找相同状态节点,搜索树变为 DAG;
-
依据 action edge(而不是 node)的访问次数来计算 PUCT;
-
反向传播过程采用增量更新:
$$ V(n) \larr \frac{1}{N(n)} \left(U(n)+\sum_c N(c)V(c)\right) $$注意 $U(n)$ 表示价值网络给出的 utility estimate,是必不可少的。
实际操作中,MCGS 在内存回收方面会比较麻烦,好在 AlphaZero 产生的搜索树不是很大,所以我直接做一遍 DFS 清理。目前训练阶段还是使用 MCTS,推理使用 MCGS。
工程优化
由于项目代码是 100% Python,要达到资源的完全利用几乎不可能。不过还是有一些技巧可以提升训练效率的。
并行自对弈
这个 idea 很好理解,也可以应用到大部分主流强化学习算法上。使用多个进程并行在不同的 GPU 上收集训练数据,并将结果发送给主进程进行模型更新。
目前,我总共使用 $20$ 个不同的进程自对弈,均匀分配到 $4$ 张卡上运行。注意要使用 torch.multiprocessing 代替 Python 内置的 multiprocessing 模块。
CUDA Graphs
这也是一个比较通用的优化技巧,在很多机器学习应用中都可以使用。其原理是将整个计算图发送到 GPU 上执行,显著减少前/后端交互和 kernel 启动开销 5。对于较小的网络和 batch_size,CUDA Graph 可以带来意料之外的速度提升。
项目根目录下提供了(简陋的)benchmark 脚本,在单张 RTX 4090 上测试结果如下(batch_size=1 模拟 self-play 环境):
| 类别 | 推理方法 | 计算速度(FPS) |
|---|---|---|
| Base | torch.no_grad |
$249.1$ |
| Base | torch.inference_mode |
$265.9$ |
| TorchScript | torch.jit.script |
$271.5$ |
| TorchScript | torch.jit.trace |
$501.4$ |
| CUDA Graphs | torch.cuda.graph |
$3184.5$ |
另外 torch.compile(mode='reduce-overhead') 也可以实现基于 CUDA Graph 的推理。不过这个 API 不支持 Windows,且编译耗时,没有 torch.cuda.graph 用的舒服。
测试结果
训练持续约 $14$ 天,共 $30000 \times 16$ 次迭代。首先是训练过程的 Loss、Entropy(策略熵)和 episode_len(自对弈棋局长度)曲线:
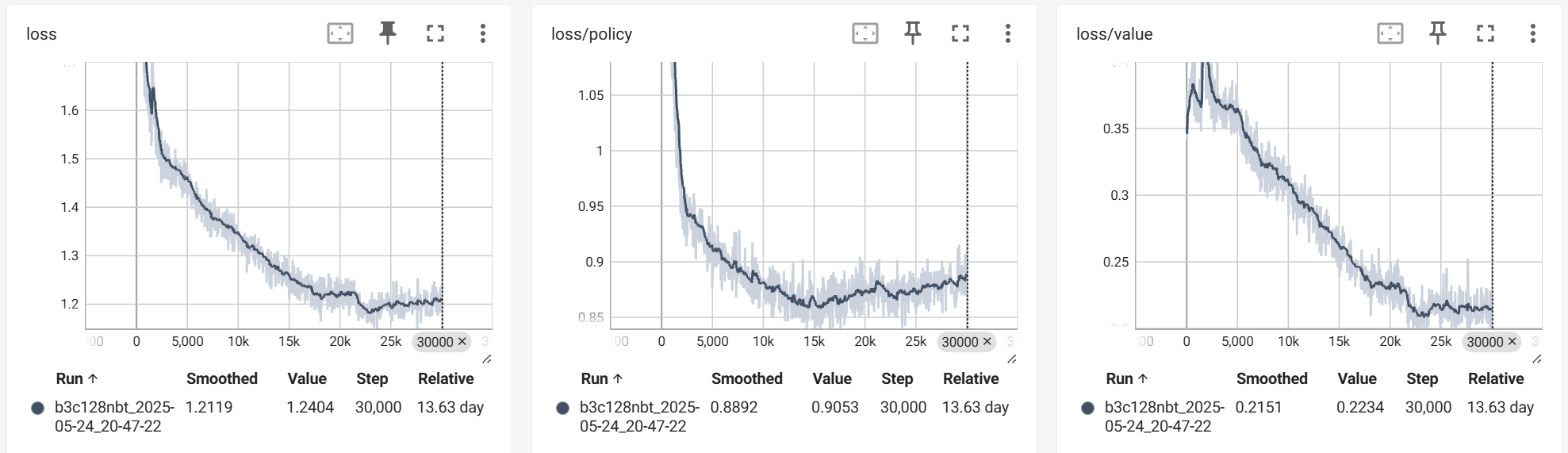
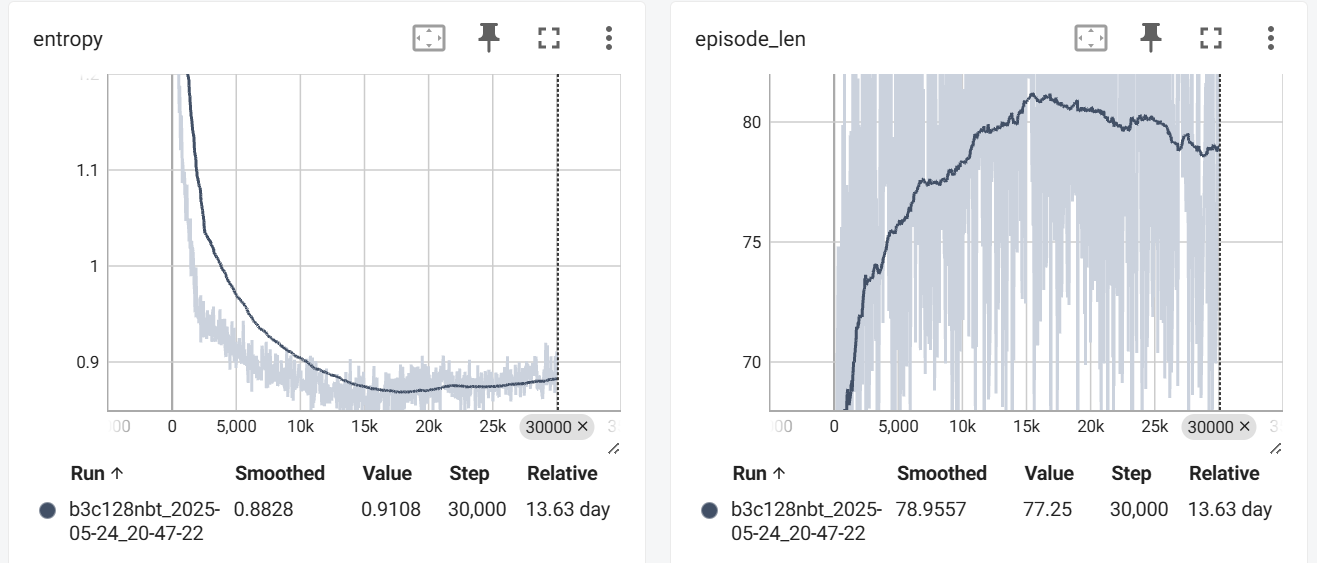
loss 和 entropy 前期快速下降,后期趋于稳定(不会向 $0$ 收敛是由于数据分布在不断改变);episode_len 前期提升,后期略有下降(可能是因为找到了更快的杀棋走法)。总体来说符合直觉,没有出现什么不同于预期的表现。
下面是 ELO6 评分曲线,体现真实棋力:
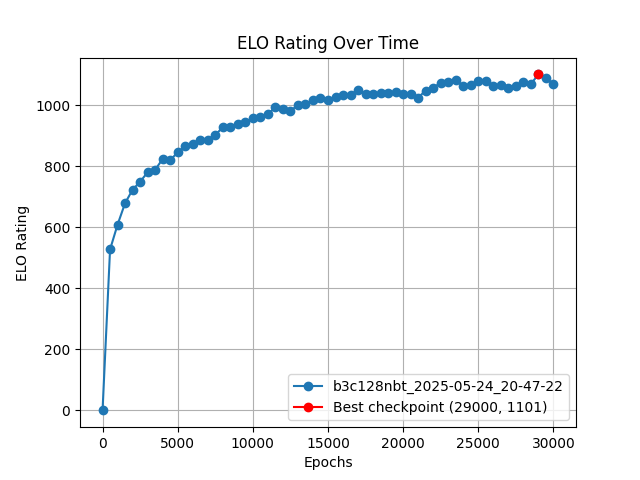
整体来看训练过程十分稳定(近似亚线性增长),最终训练基本饱和。
解决相同任务的最优传统方法在相同算力下对 katac4 的最佳检查点只有约 $26\%$ 的胜率,对应 -182 ELO 分差。画在图上可以看出,我们只用 $1/4$ 的迭代次数($3$ 天训练)就达到了与之相当的水平。
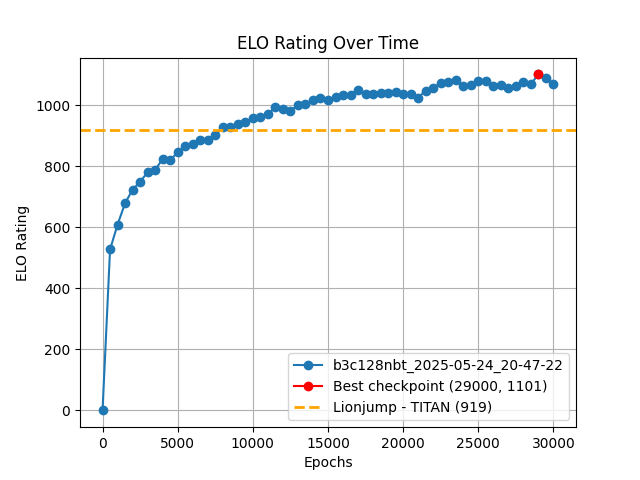
实际上这个估计并不准确——Epoch 6500 的检查点也能对其取得超过 $50\%$ 的胜率。上图仅供参考。
我非常感激这位前辈能在最近开源出他的方法;在项目开发前期,我一直很好奇他为什么能在榜上遥遥领先。前两天看了他的项目报告,真没想到传统方法用 PUCT 也比 UCT 效果更好。说实话,不让我用神经网络,估计连总榜第一页都进不去。
附上对战 Saiblo 平台样例 AI 的测试结果:
这个结果有时跑不出来,会 TLE。最强的 checkpoint 除了 TLE 之外从来就没输过(测了 $6\times100$ 场)。平台上只有 CPU,因此推理方案用的是 TorchScript。然而 import torch 和 torch.jit.load 都需要时间开销,评测机负载比较大的时候可能还没加载完模型就 TLE 了,这个我真的无能为力。(叹气)
给平台几个建议:
- 支持 LibTorch,这样我可以用 C++ 写推理,排除掉 import 时间;
- 提供一些轻量化的推理框架(比如 ONNX Runtime),也可以缓解加载缓慢问题。
- 再退一步,可以适当放宽第一步的时间限制……
另外我还搞了一个娱乐性的版本 fastc4,直接选择神经网络输出概率最大的着法。这个版本其实也不赖:
- 对样例 AI 胜率 $97\%$;
- 对 jiegec/FourChess 胜率 $65\%$;
- 对 frvdec(前榜二)胜率 $48\%$;
- 对 Lionjump0723/connect4(前榜一)胜率 $45\%$。
手动观察了一些对局,感觉神经网络更在乎长期收益——它们会为未来很多步规划,而不在乎局部得失。传统方法则天然侧重于短期算杀,而在无明显杀棋时就显得弱势很大。我的 AI 输给其他 AI 经常是在前 $25$ 步因为杀棋盲点被秒掉,但到 $50$ 步以后,局面几乎完全落入它的的控制中,传统算法由于前期规划失误后期根本无能为力。这有点类似于国际象棋引擎中 Stockfish 和 Leela Chess Zero 的区别——前者精打细算,后者更依赖直觉。
希望这些 insight 能为后续传统方法 AI 的开发提供一些帮助,也欢迎大家在平台上与 katac4 对局、测试:
- katac4(Epoch 29000):
96c96ac2389547958141d932d9279efc - katac4(Epoch 30000):
2c9bd80e1e0e480a8f32214448880a62 - katac4(Epoch 6500):
d4e85acaf1ab4025b3c6a7ebec4fd0f0 - fastc4(Epoch 29000):
941dafdce03640bfb7ceb3aa32613252
后续改进方向
现在主要问题有二:
- 硬件利用效率低;
- 模型前期盲点多。
后续会考虑将不同自对弈对局中的叶子状态合并到一个大 batch 中,应该能基本解决问题一;
对于问题二,除了扩大模型规模(预计下一个模型为 b5c128nbt)之外,还有一些有待实现的算法优化:
- 添加辅助策略头(对手下一步策略分布、棋局最后落子点、soft policy)帮助训练;
- 优化棋盘状态表示(前面更多手的落子位置、棋子成二成三的位置等);
- Playout Cap Randomization 的 fast game policy sample 要弃掉;
- 正比于 $D_\mathrm{KL}(\hat{\boldsymbol\pi}||\boldsymbol\pi)$ 进行 importance sampling,重点训练预测错误的位置;
- Batch Norm 替换成 Batch Renorm,防止模型训练和推理的行为不一致。
这个暑假如果有空会来实现一些。各位若有兴趣也可以 PR 实现改进。随时欢迎!
拓展阅读
- Mastering the game of Go without human knowledge
- Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm
- Accelerating Self-Play Learning in Go
- Other Methods Implemented in KataGo
- 圍棋引擎 Sayuri 開發日誌
-
原版 AlphaZero 中直接预测局面价值 $V(s_t) \in [-1,1]$ 并使用 MSE Loss,这里沿用了 KataGo 和 Leela Zero 的改进做法。 ↩︎
-
神经网络设计也参考了 KataGo,使用了全局池化(Global Pooling)和 Nested Bottleneck Residual Nets。现在的版本命名为
b3c128nbt,表示 $3$ 个 $128$ 通道的 nested bottleneck 残差块。出于篇幅考虑,这里不具体介绍模型方面的设计优化,感兴趣的读者可自行翻阅代码。 ↩︎ -
我的代码实现没有做到这一点,看起来影响并不大。不过把它们去掉应该是更好的选择,后续计划测试。 ↩︎