A. Cow and Haybales
题面
The USA Construction Operation (USACO) recently ordered Farmer John to arrange a row of n haybale piles on the farm. The $i$-th pile contains $a_i$ haybales.
However, Farmer John has just left for vacation, leaving Bessie all on her own. Every day, Bessie the naughty cow can choose to move one haybale in any pile to an adjacent pile. Formally, in one day she can choose any two indices $i$ and $j$ ($1\le i,j\le n$) such that $|i−j|=1$ and $a_i > 0$ and apply $a_i=a_i−1$, $a_j = a_j + 1$. She may also decide to not do anything on some days because she is lazy.
Bessie wants to maximize the number of haybales in pile $1$ (i.e. to maximize $a_1$), and she only has $d$ days to do so before Farmer John returns. Help her find the maximum number of haybales that may be in pile $1$ if she acts optimally!
输入
The input consists of multiple test cases. The first line contains an integer $t$ ($1\le t\le 100$) — the number of test cases. Next $2t$ lines contain a description of test cases — two lines per test case.
The first line of each test case contains integers $n$ and $d$ ($1\le n,d\le 100$) — the number of haybale piles and the number of days, respectively.
The second line of each test case contains $n$ integers $a_1,a_2,\dots,a_n$ $(0\le a_i\le 100)$ — the number of haybales in each pile.
输出
For each test case, output one integer: the maximum number of haybales that may be in pile $1$ after $d$ days if Bessie acts optimally.
样例
输入
|
|
输出
|
|
注释
In the first test case of the sample, this is one possible way Bessie can end up with $3$ haybales in pile $1$:
- On day one, move a haybale from pile $3$ to pile $2$
- On day two, move a haybale from pile $3$ to pile $2$
- On day three, move a haybale from pile $3$ to pile $1$
- On day four, move a haybale from pile $2$ to pile $1$
- On day five, do nothing
In the second test case of the sample, Bessie can do nothing on the first day and move a haybale from pile $2$ to pile $1$ on the second day.
解题思路
贪心算法:先把第二堆的移到第一堆,再把第三堆的移到第一堆,……
题目中的样例解释有点误导(:()
代码
|
|
B. Cow and Friend
题面
Bessie has way too many friends because she is everyone’s favorite cow! Her new friend Rabbit is trying to hop over so they can play!
More specifically, he wants to get from $(0,0)$ to $(x,0)$ by making multiple hops. He is only willing to hop from one point to another point on the 2D plane if the Euclidean distance between the endpoints of a hop is one of its n favorite numbers: $a_1,a_2,…,a_n$. What is the minimum number of hops Rabbit needs to get from $(0,0)$ to $(x,0)$? Rabbit may land on points with non-integer coordinates. It can be proved that Rabbit can always reach his destination.
Recall that the Euclidean distance between points $(x_i,y_i)$ and $(x_j,y_j)$ is $\sqrt{(x_i−x_j)^2+(y_i−y_j)^2}$.
For example, if Rabbit has favorite numbers 1 and 3 he could hop from $(0,0)$ to $(4,0)$ in two hops as shown below. Note that there also exists other valid ways to hop to $(4,0)$ in $2$ hops (e.g. $(0,0)\to(2, \sqrt 5)\to(4,0)$).
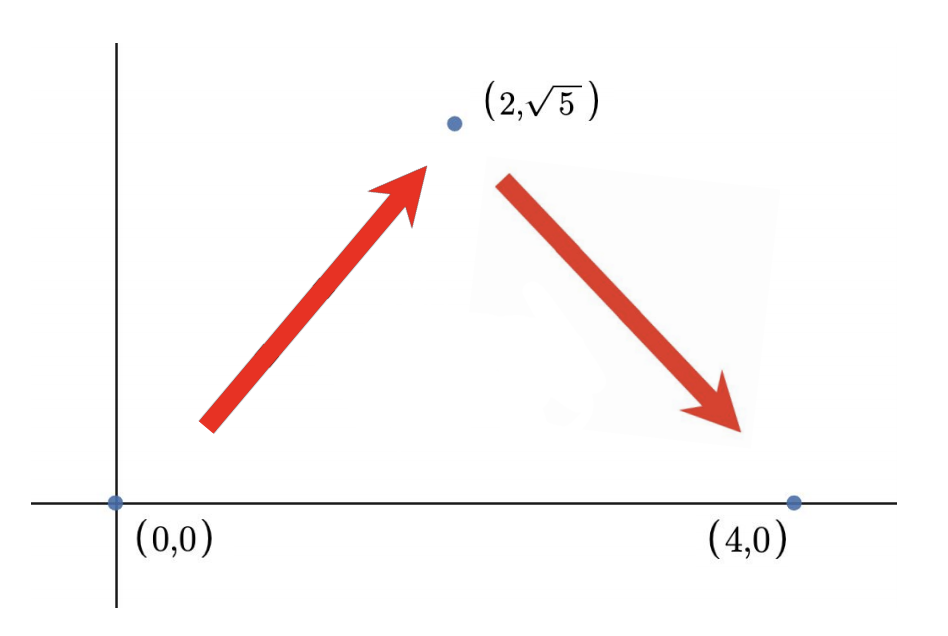
Here is a graphic for the first example. Both hops have distance $3$, one of Rabbit’s favorite numbers.
In other words, each time Rabbit chooses some number $a_i$ and hops with distance equal to $a_i$ in any direction he wants. The same number can be used multiple times.
输入
The input consists of multiple test cases. The first line contains an integer $t$ ($1\le t\le 1000$) — the number of test cases. Next $2t$ lines contain test cases — two lines per test case.
The first line of each test case contains two integers $n$ and $x$ ($1\le n\le 10^5$, $1\le x\le 10^9$) — the number of favorite numbers and the distance Rabbit wants to travel, respectively.
The second line of each test case contains $n$ integers $a_1, a_2, \dots, a_n$ ($1\le a_i \le 10^9$) — Rabbit’s favorite numbers. It is guaranteed that the favorite numbers are distinct.
It is guaranteed that the sum of $n$ over all the test cases will not exceed $10^5$.
输出
For each test case, print a single integer — the minimum number of hops needed.
样例
输入
|
|
输出
|
|
注释
The first test case of the sample is shown in the picture above. Rabbit can hop to $(2, \sqrt 5)$, then to $(4,0)$ for a total of two hops. Each hop has a distance of $3$, which is one of his favorite numbers.
In the second test case of the sample, one way for Rabbit to hop $3$ times is: $(0,0) → (4,0) → (8,0) → (12,0)$.
In the third test case of the sample, Rabbit can hop from $(0,0)$ to $(5,0)$.
In the fourth test case of the sample, Rabbit can hop: $(0,0) → (5,10\sqrt2) → (10,0)$.
解题思路
纯数学!!!
代码
|
|
C. Cow and Message
题面
Bessie the cow has just intercepted a text that Farmer John sent to Burger Queen! However, Bessie is sure that there is a secret message hidden inside.
The text is a string $S$ of lowercase Latin letters. She considers a string $t$ as hidden in string $S$ if $t$ exists as a subsequence of $S$ whose indices form an arithmetic progression. For example, the string aab is hidden in string aaabb because it occurs at indices $1$, $3$, and $5$, which form an arithmetic progression with a common difference of $2$. Bessie thinks that any hidden string that occurs the most times is the secret message. Two occurrences of a subsequence of $S$ are distinct if the sets of indices are different. Help her find the number of occurrences of the secret message!
For example, in the string aaabb, a is hidden $3$ times, b is hidden $2$ times, ab is hidden $6$ times, aa is hidden $3$ times, bb is hidden $1$ time, aab is hidden $2$ times, aaa is hidden $1$ time, abb is hidden $1$ time, aaab is hidden $1$ time, aabb is hidden $1$ time, and aaabb is hidden $1$ time. The number of occurrences of the secret message is $6$.
输入
The first line contains a string $S$ of lowercase Latin letters ($1\le |S|\le 105$) — the text that Bessie intercepted.
输出
Output a single integer — the number of occurrences of the secret message.
样例
输入 #1
|
|
输出 #1
|
|
输入 #2
|
|
输出 #2
|
|
输入 #3
|
|
输出 #3
|
|
注释
In the first example, these are all the hidden strings and their indice sets:
aoccurs at $(1), (2), (3)$boccurs at $(4), (5)$aboccurs at $(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)$aaoccurs at $(1,2), (1,3), (2,3)$bboccurs at $(4,5)$aaboccurs at $(1,3,5), (2,3,4)$aaaoccurs at $(1,2,3)$abboccurs at $(3,4,5)$aaaboccurs at $(1,2,3,4)$aabboccurs at $(2,3,4,5)$aaabboccurs at $(1,2,3,4,5)$
Note that all the sets of indices are arithmetic progressions.
In the second example, no hidden string occurs more than once.
In the third example, the hidden string is the letter l.
解题思路
动态规划
代码
|
|