前言
好久没更算法笔记专栏了，正好学了新算法来更新……
这也是本专栏的第一个专题问题，涉及到三种数据结构，如果写得有问题请各位大佬多多指教，谢谢！
关于 RMQ 问题
RMQ 的全称是 Range Minimum/Maximum Query，即区间最大/最小值问题。
本文中，我们的算法以求最大值为例（最小值基本一致）。题面如下：
给定一个长为$N$的序列$A=(A_1,A_2,\dots,A_N)$。
有$Q$个询问，第$i$个询问如下：
$\to~$给定$1\le l_i\le r_i\le N$，求区间$[l_i,r_i]$的最大值，即$\displaystyle\max_{j=l_i}^{r_i} A_j$。
下面，我们将从暴力算法开始，逐步讲解 RMQ 问题的常用解法。
通用的 RMQ 问题（除暴力外所有算法都能通过）：
解法
暴力法
我们先读取序列$A$，再逐个读取询问，对于每个询问直接遍历$A_l\dots A_r$，最终输出结果。
总时间复杂度为$\mathcal O(\sum r_i-l_i)=\mathcal O(NQ)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include <cstdio>
#define maxn 100005
using namespace std;
int a[maxn];
int main()
{
int n, q;
scanf("%d%d", &n, &q);
for(int i=0; i<n; i++)
scanf("%d", a + i);
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
l --, r --;
int res = a[l];
for(int i=l+1; i<=r; i++)
if(a[i] < res)
res = a[i];
printf("%d ", res);
}
return 0;
}
|
然而，当你提交到洛谷 P1816时……
肯定还是时间复杂度的锅，算法需要进一步优化。
Sparse Table
Sparse Table（以下称ST表）是用于静态求解 RMQ 问题的数据结构。
静态求解是指在原始序列不改变的情况下求解问题。或者说，ST表不能直接进行修改操作。
ST表的初始化时间复杂度为$\mathcal O(N\log N)$，单次查询时间复杂度为$\mathcal O(1)$。
存储结构
$$
st[i][j]=\max\{A_i,A_{i+1},\dots,A_{i+2^j-1}\}
$$
也就是说，$st[i][j]$表示从$A_i$开始，$2^j$个元素中的最大值。这运用了倍增的思想。
下面考虑如何快速初始化整个数组。
初始化
$$
st[i][j]=\max\{st[i][j-1],st[i+2^{j-1}][j-1]\}
$$
填表时，先枚举$j$，再枚举$i$。由于整个表共有大约$N\log N$个状态，而计算一个状态值的时间复杂度为$\mathcal O(1)$，所以初始化的总时间复杂度为$\mathcal O(N\log N)$。
伪代码如下：
1
2
3
4
5
6
7
|
function init() {
for i = 1 to N
st[i][0] = A[i]
for j = 1 to log2(N)
for i = 1 to (N + 1 - 2^j)
st[i][j] = max(st[i][j - 1], st[i + 2^(j-1)][j - 1])
}
|
C++ 实现：
1
2
3
4
5
6
7
8
|
void init()
{
for(int i=0; i<n; i++)
st[i][0] = A[i];
for(int j=1; j<=log2(n); j++)
for(int i=0; i+(1<<j)<=n; i++) // 注意必须是<=n，1<<j即为2^j
st[i][j] = max(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
|
查询
对于$[l,r)$区间的 RMQ 查询，根据ST表的原理，我们要找到两个区间$[l,a)$和$[b,r)$，使得它们的并集正好为$[l,r)$。即：$l\le b\le a\le r$。
为什么是并集?
$\to~$因为$\max(a,a)=a$，所以重复的不影响结果。
$\to~$如果出现遗漏，且遗漏的正好为最大/最小值，那会影响最终结果，所以不能遗漏。
$\to~$如果检查到了多余的元素，且多余的正好大于原区间的最大值，会使查询结果变大，所以不能有多余。
综上，必须满足$[l,a)$和$[b,r)$的并集正好为$[l,r)$才能查询。
要满足上述条件，我们可以让$a$尽可能靠近$r$，让$b$尽可能靠近$l$，来达到这样的效果。
此时，我们还需要满足并集的条件$l\le a,b\le r$，因此我们需要找到最大的$k$，使得$a=l+2^k$，$b=r-2^k$。
$$
\left\{ \begin{array}{c}
l+2^k\le r \\
r-2^k\ge l
\end{array} \right.~~\to~~ 2^k\le r-l\\
~\\
\to~k\le \log_2(r-l)
$$
又因为$k$必须是整数，所以取$k=\lfloor\log_2(r-l)\rfloor$即可。
1
2
3
4
5
6
|
// query(l, r) = max(A[l], ..., A[r - 1])
inline int query(int l, int r)
{
int k = log2(r - l);
return max(st[l][k], st[r - (1 << k)][k]);
}
|
完整实现
下面给出用Sparse Table解决例题的完整代码。总时间复杂度为$\mathcal O(Q+N\log N)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <cstdio>
#include <cmath>
#include <algorithm>
#define maxn 100005
using namespace std;
int st[maxn][17]; // 2^17=131072
void init(int n)
{
for(int j=1, t=log2(n); j<=t; j++)
for(int i=0; i+(1<<j)<=n; i++)
st[i][j] = min(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
inline int query(int l, int r)
{
int k = log2(r - l);
return min(st[l][k], st[r - (1 << k)][k]); // 注意此题为min，不是求max
}
int main()
{
int n, q;
scanf("%d%d", &n, &q);
for(int i=0; i<n; i++)
scanf("%d", st[i]); // 直接读入到ST表中，节约时间和空间
init(n);
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
// 此处注意因为是左闭右开区间[l,r)，所以只有l需要-1
printf("%d ", query(--l, r));
}
return 0;
}
|
运行时间：$128\mathrm{ms}$
使用内存：$6.90\mathrm{MB}$
树状数组
关于树状数组的原理我已经在这篇文章中讲过，这里不再多说了。下面我们考虑如何应用树状数组解决 RMQ 问题。
原算法
树状数组可以用lowbit操作实现prefixSum（前缀和）以及update（更新）操作，时间复杂度均为$\mathcal O(N\log N)$。不仅是加法，对于任意满足结合律的运算这两种操作都有效。
我们来简单实现一下支持prefixMax和update操作的树状数组：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#define INF 2147483647
#define lowbit(x) ((x) & -(x))
inline void setmax(int& x, int y) { if(y > x) x = y; }
int n, A[N], bit[N];
// max(A[1], ..., A[i])
inline int prefixMax(int i)
{
int res = -INF;
for(; i>0; i-=lowbit(i))
setmax(res, bit[i]);
return res;
}
// A[i] = max(A[i], val)
inline void update(int i, int val)
{
for(; i<=n; i+=lowbit(i))
setmax(bit[i], val);
}
|
若要初始化树状数组，可以利用update操作进行$\mathcal O(N\log N)$的初始化：
1
2
3
4
5
6
7
|
inline void init()
{
for(int i=1; i<=n; i++)
bit[i] = -INF; // 这一段不要忘！
for(int i=1; i<=n; i++)
update(i, A[i]);
}
|
另外，我们也可以用子节点直接更新父节点，达到$\mathcal O(N)$建树的效果：
1
2
3
4
5
6
7
8
9
10
|
inline void init()
{
for(int i=1; i<=n; i++)
bit[i] = A[i];
for(int i=1; i<=n; i++)
{
int j = i + lowbit(i);
if(j <= n) setmax(bit[j], bit[i]);
}
}
|
考虑加法时我们计算rangeSum（区间和）的算法：
1
2
3
4
|
inline int rangeSum(int l, int r)
{
return prefixSum(r) - prefixSum(l - 1);
}
|
也就是用$(A_1+A_2+\dots+A_r)-(A_1+A_2+\dots+A_{l-1})=A_l+\dots+A_r$。
现在回过来考虑 RMQ 的查询，Min/Max运算不可逆，所以很明显不能用这种计算方式。
下面我们来介绍针对 RMQ 的树状数组设计。
RMQ 树状数组
$$
f(l,r)=\begin{cases}
\max\{B_r,f(l,t)\} & (t\ge l)\\
\max\{A_r,f(l,r-1)\} & (t
等式$1$ 证明
根据树状数组的定义，$B_i=\max\{A_{i-\mathrm{lowbit}(i)+1},\dots,A_i\}=f(i-\mathrm{lowbit}(i)+1,i)$。
又有$f(l,r)=\max\{f(l,t),f(t+1,r)\}$，由于$f(t+1,r)=f(r-\mathrm{lowbit}(r)+1,r)=B_r$，所以当$t\ge l$时，$f(l,r)=\max\{B_r,f(l,t)\}$。
等式$2$ 证明
根据$\max$操作的结合律可得：$f(l,r)=\max\{f(l,r-1),f(r,r)\}=\max\{f(l,r-1),A_r\}$。
这个等式对于任意$r$都成立，但出于时间考虑，我们尽可能使用等式$1$（如果全用等式$2$就退化成了$\mathcal O(N)$的暴力）。
代码实现：
1
2
3
4
5
6
7
8
|
int rangeMax(int l, int r)
{
if(l == r) return A[l];
int t = r - lowbit(r);
return t < l?
max(A[r], rangeMax(l, r - 1)):
max(bit[r], rangeMax(l, t));
}
|
这种查询方式的时间复杂度不好估算，可粗略地记为$\mathcal O(\log N)$。实际情况下，运行时间可能稍大于这个值。
另外，此算法对任意满足结合律的运算（如gcd，lcm）都有效。
完整实现
下面给出用树状数组解决例题的完整代码。总时间复杂度为$\mathcal O(N+Q\log N)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <cstdio>
#include <algorithm>
#define maxn 100005
using namespace std;
#define lowbit(x) ((x) & -(x))
int a[maxn], bit[maxn];
int rangeMin(int l, int r)
{
if(l == r) return a[l];
int t = r - lowbit(r);
return t < l?
min(a[r], rangeMin(l, r - 1)):
min(bit[r], rangeMin(l, t));
}
inline void init(int n)
{
for(int i=1; i<=n; i++)
bit[i] = a[i];
for(int i=1; i<=n; i++)
{
int j = i + lowbit(i);
if(j <= n)
bit[j] = min(bit[j], bit[i]);
}
}
int main()
{
int n, q;
scanf("%d%d", &n, &q);
for(int i=1; i<=n; i++)
scanf("%d", a + i);
init(n);
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d ", rangeMin(l, r));
}
return 0;
}
|
运行时间：$207\mathrm{ms}$
使用内存：$1.10\mathrm{MB}$
另外，我们还可以把rangeMin写成非递归的形式，以进一步节省运行时间：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <cstdio>
#define maxn 100005
using namespace std;
#define INF 2147483647
#define lowbit(x) ((x) & -(x))
inline void setmin(int& x, int y) { if(y < x) x = y; }
int a[maxn], bit[maxn];
int rangeMin(int l, int r)
{
int res = INF;
while(l <= r)
{
int t = r - lowbit(r);
if(t < l) setmin(res, a[r--]);
else setmin(res, bit[r]), r = t;
}
return res;
}
inline void init(int n)
{
for(int i=1; i<=n; i++)
bit[i] = a[i];
for(int i=1; i<=n; i++)
{
int j = i + lowbit(i);
if(j <= n) setmin(bit[j], bit[i]);
}
}
int main()
{
int n, q;
scanf("%d%d", &n, &q);
for(int i=1; i<=n; i++)
scanf("%d", a + i);
init(n);
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d ", rangeMin(l, r));
}
return 0;
}
|
运行时间：$135\mathrm{ms}$
使用内存：$1.14\mathrm{MB}$
线段树
线段树和树状数组一样，都是解决区间问题的树状结构。不过线段树的应用范围更加广泛，时间复杂度与树状数组基本一致，但每种操作都有一个$3\thicksim4$之间的常数。线段树建树（初始化）的时间复杂度为$\mathcal O(N)$，单次区间查询的时间复杂度为$\mathcal O(\log N)$。
RMQ 问题不涉及修改操作，因此我们暂时不考虑这种操作。
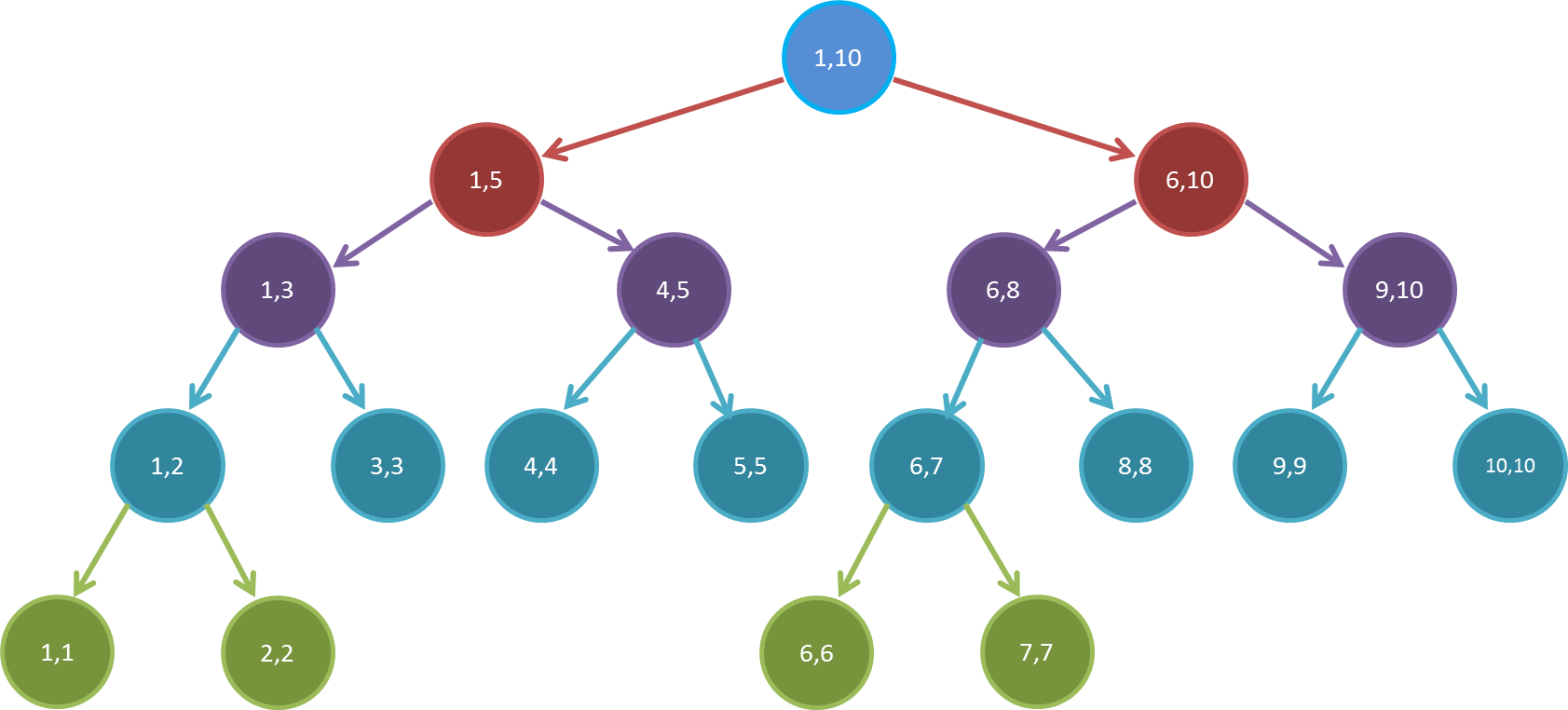
如图即为$N=10$的一棵线段树。可以发现，线段树本质上是一棵二叉树，每个结点代表一个区间，其存储的值为这个区间的区间和（在 RMQ 问题中为区间最大/最小值）。一个结点的左儿子结点和右儿子结点对应区间的并集正好为这个结点对应的区间（叶子结点除外），且左右两区间的长度的差值不超过$1$。
从树的角度考虑，$n_1=0$，即没有子结点数量为$1$的结点。
一般的，若一个结点对应的区间为$[l,r]$：
- $l = r$：此结点为叶子结点。
- $l < r$，令$m=\lfloor\frac{l+r}2\rfloor$：
- 左子结点对应的区间为$[l,m]$。
- 右子结点对应的区间为$[m+1,r]$。
顺便纠正一下线段树的几个误区：
线段树是一棵完全二叉树。
请仔细看看图。
线段树是一棵二叉搜索树。
反正我是没找到哪里这样定义的。百度百科 OI Wiki
线段树上同一深度的结点所对应的区间长度一定相等。
看看图，$[1,3]$和$[4,5]$两个区间，长度明显不相等。
特例：当$N$是$2$的整数次幂时，这句话一定成立。
存储结构
线段树采用堆式储存法，根结点为$1$，结点$u$的父亲为$\lfloor\frac u2\rfloor$，左子结点为$2u$，右子结点为$2u+1$。
可以用位运算优化：
- $u$的父亲：$\lfloor\frac u2\rfloor=~$
u >> 1
- $u$的左儿子：$2u=~$
u << 1
- $u$的右儿子：$2u+1=~$
u << 1 | 1（或u << 1 ^ 1）
1
2
3
4
5
6
7
8
|
// 数组定义
int a[N], c[4 * N];
// 宏定义
#define INF 2147483647
#define ls(x) (x << 1) // 左儿子结点
#define rs(x) (x << 1 | 1) // 右儿子结点
#define par(x) (x >> 1) // 父亲结点
|
下文中，我们令$N$表示元素个数，$A$表示原数组，$C$表示线段树（数组形式存储）。
可以证明，线段树的结点个数不会超过$4N-5$，所以我们可以把$C$的长度设为$4N$。
建树（初始化）
对于一个结点数据的计算，我们可以先递归地初始化其左子树，再到右子树，最后两儿子的数据取$\max$即可。
代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// 结点p, 区间[l, r]建树
void build(int l, int r, int p)
{
if(l == r)
{
c[p] = a[l];
return;
}
int m = l + r >> 1;
build(l, m, ls(p));
build(m + 1, r, rs(p));
c[p] = max(c[ls(p)], c[rs(p)]);
}
|
区间查询
同样采用递归的方式，设$p$为当前结点，$[l,r]$为当前结点区间，$[a,b]$为当前查询区间，函数返回$[l,r]$和$[a,b]$的交集的区间和：
- 如果$[l,r]$是$[a,b]$的子集（$a\le l\le r\le b$），直接返回当前结点对应的区间和。
- 否则，递归查询左右子树，如果没有交集则不查询。返回查询的子树的最大值。
如果上面不是很好理解，可以直接看代码实现：
1
2
3
4
5
6
7
8
9
10
|
// 结点p, 查询区间[a, b], 当前区间[l, r]
int query(int l, int r, int a, int b, int p)
{
if(a <= l && r <= b) return c[p];
int m = l + r >> 1, res = -INF;
if(m >= a) res = max(res, query(l, m, a, b, ls(p)));
// m + 1 <= b 即为 m < b
if(m < b) res = max(res, query(m + 1, r, a, b, rs(p)));
return res;
}
|
完整实现
下面给出用线段树解决例题的完整代码。总时间复杂度为$\mathcal O(N+Q\log N)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <cstdio>
#include <algorithm>
#define maxn 100005
using namespace std;
#define INF 2147483647
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
#define par(x) (x >> 1)
int a[maxn], c[maxn << 2];
void build(int l, int r, int p)
{
if(l == r)
{
c[p] = a[l];
return;
}
int m = l + r >> 1;
build(l, m, ls(p));
build(m + 1, r, rs(p));
c[p] = min(c[ls(p)], c[rs(p)]);
}
int query(int l, int r, int a, int b, int p)
{
if(a <= l && r <= b) return c[p];
int m = l + r >> 1, res = INF;
if(m >= a) res = min(res, query(l, m, a, b, ls(p)));
if(m < b) res = min(res, query(m + 1, r, a, b, rs(p)));
return res;
}
int main()
{
int n, q;
scanf("%d%d", &n, &q);
for(int i=0; i<n; i++)
scanf("%d", a + i);
build(0, n - 1, 1);
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d ", query(0, n - 1, --l, --r, 1));
}
return 0;
}
|
运行时间：$163\mathrm{ms}$
使用内存：$1.78\mathrm{MB}$
总结
我们来对比一下四种算法，从理论的角度：
| 算法 |
预处理时间复杂度 |
单次查询时间复杂度 |
空间复杂度 |
符合题目要求？ |
| 暴力 |
$\mathcal O(1)$ |
$\mathcal O(N)$ |
$\mathcal O(N)$ |
❌ |
| ST表 |
$\mathcal O(N\log N)$ |
$\mathcal O(1)$ |
$\mathcal O(N\log N)$ |
✔️ |
| 树状数组 |
$\mathcal O(N)$或$\mathcal O(N\log N)$ |
$\mathcal O(\log N)$ |
$\mathcal O(N)$ |
✔️ |
| 线段树 |
$\mathcal O(N)$ |
$\mathcal O(\log N)$ |
$\mathcal O(N)$ |
✔️ |
从洛谷 P1816上实际运行情况的角度（暴力TLE，不考虑）：
| 算法 |
运行时间 |
内存占用 |
代码长度 |
| ST表 |
$128\mathrm{ms}$ |
$6.90\mathrm{MB}$ |
$625\mathrm B$ |
| 树状数组（递归） |
$207\mathrm{ms}$ |
$1.10\mathrm{MB}$ |
$720\mathrm B$ |
| 树状数组（非递归） |
$135\mathrm{ms}$ |
$1.14\mathrm{MB}$ |
$786\mathrm B$ |
| 线段树 |
$163\mathrm{ms}$ |
$1.78\mathrm{MB}$ |
$905\mathrm B$ |
可以看出，ST表写起来简单省事，运行时间也是最快，不过内存占用稍高，毕竟空间复杂度是$\mathcal O(N\log N)$；
树状数组可以说是均衡了时间与空间，尽量使用非递归查询，比递归速度快$53\%$，当然如果想省事也可以使用递归式查询；
线段树可以说是完全输给了树状数组（非递归），不过线段树功能比较多，用来做 RMQ 可以说是大材小用。所以线段树在 RMQ 问题中没什么优势，有一些缺点还是可以理解的。
本文到此结束，希望大家给个三连！
这也是我在$2023$年写的第一篇文章（也是我的第一篇万字长文），祝大家新年快乐！