前言
生活中经常遇到类似这种的问题:
公路修建
有一些城市,城市之间要修建高速公路,每两个城市之间都可以修双向的路。其中每两个城市之间修路都需要花费对应的金额。请问如何修路,使得总花费的金额最少,且任意两个城市之间都可以直接或间接通过修建的路来通行?
实际上,我们可以把这种问题抽象化,把城市看作图的顶点,公路看作带权的无向边,这样整个国家就被抽象成了一张带权无向图。又因为要求总花费最小,所以修的路一定组成一棵生成树,于是转换成下面的问题:
给定一张带权无向图$G$,求它的一棵生成树,使其中所有边权之和最小。
实际上,这就是大名鼎鼎的「最小生成树问题」。
比如看下面这张图:
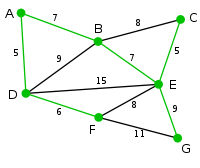
其中,标绿的部分即为其最小生成树。
对于这种问题,很多数学家都有所研究。但毕竟是数学家,不懂计算机,就只管算法的正确性,不管实现起来的简单性、可行性和效率,所以很多算法都被人们所抛弃。不过,还是有两种算法脱颖而出,它们就是标题中的——Kruskal 和 Prim。
模板:洛谷 P3366【模板】最小生成树
数据范围:$N\le5000,M\le2\times10^5,w\le 10^4$。
Kruskal
Kruskal算法是由Joseph Kruskal于1956年提出的最小生成树算法,时间复杂度为$\mathcal O(m\log m)$。下面来看这种算法的流程。
Kruskal 算法流程
- 将所有边按权值从小到大排序,依次遍历每一条边;
- 对于每一条边,如果在当前子图中连上之后不会形成环,则选择这条边作为最小生成树的一部分,加入子图;
- 选择$N-1$条边后即可结束算法。
并查集 - 加快算法速度
在正式实现Kruskal算法之前,我们还需要先了解一下并查集。如果判定是否会出现环的部分使用$\text{DFS}$,则时间复杂度为$\mathcal O(nm+m\log m)$,费时费力。若使用并查集来实现,则代码非常简单,且时间复杂度仅为$\mathcal O(m\log m)$(排序的耗时)。并查集模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class dsu
{
private:
const int n;
int* fa;
public:
inline dsu(int count): n(count) // 初始化大小为n的并查集
{
fa = new int[n]; // 申请新的内存
for(int i=0; i<n; i++)
fa[i] = i; // 初始化fa[i]=i
}
inline ~dsu() { delete[] fa; } // 销毁存储空间,防止内存泄露
inline int size() { return n; } // 返回并查集大小
int find(int x) { return fa[x] == x? x: fa[x] = find(fa[x]); } // 查找父亲+路径压缩
inline bool same(int x, int y) { return find(x) == find(y); } // x,y是否在同一个连通分量里?
inline void merge(int x, int y) { fa[find(x)] = find(y); } // 合并x、y,即连接x<->y这条双向边
inline bool connected() // 判断整个图是否连通
{
int p = find(0);
for(int i=0; i<n; i++)
if(find(i) != p)
return false;
return true;
}
};
|
使用并查集后,算法时间复杂度降到$\mathcal O(m\log m)$,即排序的时间复杂度。下面来看代码。
参考代码
如果对并查集不熟悉的读者可以先复制模板写代码,后面再仔细研究TA
单次Kruskal算法的排序建议用priority_queue(比sort效率更高),如果要多次Kruskal则需要提前排好序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
#include <cstdio>
#include <queue>
using namespace std;
// 代表一条边,方便排序
struct Edge
{
int from, to, weight;
inline bool operator <(const Edge& e2) const
{
return weight > e2.weight; // 注意:使用优先队列时要把大小倒过来过来
}
inline void read()
{
scanf("%d%d%d", &from, &to, &weight);
from --, to --;
}
};
// 并查集模板
class dsu
{
private:
const int n;
int* fa;
public:
inline dsu(int count): n(count)
{
fa = new int[n];
for(int i=0; i<n; i++)
fa[i] = i;
}
inline ~dsu() { delete[] fa; }
inline int size() { return n; }
int find(int x) { return fa[x] == x? x: fa[x] = find(fa[x]); }
inline bool same(int x, int y) { return find(x) == find(y); }
inline void merge(int x, int y) { fa[find(x)] = find(y); }
inline bool connected()
{
int p = find(0);
for(int i=0; i<n; i++)
if(find(i) != p)
return false;
return true;
}
};
int main()
{
int n, m;
scanf("%d%d", &n, &m); // 读入顶点数和边数
priority_queue<Edge> q; // 初始化优先队列,用于排序
while(m--)
{
Edge e;
e.read(); // 读入一条边
q.push(e); // 放入队列进行排序
}
int ans = 0, // 记录总权值
cnt = 0; // 当前选择边的个数
dsu d(n); // 初始化并查集
while(!q.empty() && cnt < n - 1) // 遍历所有边,选择了n-1条边即可退出
{
auto [u, v, w] = q.top(); q.pop(); // 弹出边权最小的边
if(!d.same(u, v)) // 如果连通后不会形成环
{
d.merge(u, v); // 连上这条边
ans += w, cnt ++; // 更新答案和计数
}
}
if(cnt == n - 1) printf("%d\n", ans); // 如果最终选择了n-1条边,输出答案
else puts("orz"); // 否则...
return 0;
}
|
最后一段也可以写成这样(不用cnt计数,输出答案时判定连通,速度稍慢):
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int ans = 0;
dsu d(n);
while(!q.empty())
{
auto [u, v, w] = q.top(); q.pop();
if(!d.same(u, v))
{
d.merge(u, v);
ans += w;
}
}
if(d.connected()) printf("%d\n", ans);
else puts("orz");
|
Prim
Prim算法于1930年由捷克数学家Vojtěch Jarník发现,在1957年又由美国计算机科学家Robert C. Prim独立发现。1959年,Edsger Wybe Dijkstra(没错,就是Dijkstra算法的发明者)再次发现了该算法。因此,在某些场合,Prim算法又被称为DJP算法、Jarník算法或Prim-Jarník算法。
Prim 算法流程
Prim与Dijkstra很相似,将顶点分为$S$和$T$两个集合,具体流程如下:
- 初始时,所有顶点全部在$S$中,$T$为空集。
- 从$S$中选择任意顶点,移动到集合$T$;
- 重复以下步骤,直到所有顶点都在$T$中:
- 选择一条边$(u,v,w)$,使得$u$在点集$S$中,$v$在点集$T$中,且权值$w$最小;
- 将这条边加入最小生成树,并将$u$移入点集$T$。
Prim算法的原始写法就不多说了,这里和Dijkstra一样,介绍priority_queue和set优化。
优先队列优化
运行时间:$328\mathrm{ms}$
时间复杂度:$\mathcal O(n\log m)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include <cstdio>
#include <queue>
#define maxn 5005
#define INF 2147483647
using namespace std;
using pii = pair<int, int>;
vector<pii> G[maxn];
int dis[maxn];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
while(m--)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
G[--u].emplace_back(--v, w);
G[v].emplace_back(u, w);
}
for(int i=1; i<n; i++)
dis[i] = INF;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.emplace(0, 0);
int ans = 0, left = n;
while(!q.empty() && left > 0)
{
auto [d, v] = q.top(); q.pop();
if(d != dis[v]) continue;
dis[v] = -INF, left --, ans += d;
for(auto [u, w]: G[v])
if(w < dis[u])
q.emplace(dis[u] = w, u);
}
if(left) puts("orz");
else printf("%d\n", ans);
return 0;
}
|
set优化
运行时间:$351\mathrm{ms}$
时间复杂度:$\mathcal O(n\log n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include <cstdio>
#include <vector>
#include <set>
#define maxn 5005
#define INF 2147483647
using namespace std;
using pii = pair<int, int>;
vector<pii> G[maxn];
int dis[maxn];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
while(m--)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
G[--u].emplace_back(--v, w);
G[v].emplace_back(u, w);
}
for(int i=1; i<n; i++)
dis[i] = INF;
set<pii> s;
s.emplace(0, 0);
int ans = 0, left = n;
while(!s.empty() && left > 0)
{
auto it = s.begin();
auto [d, v] = *it; s.erase(it);
dis[v] = -INF, left --, ans += d;
for(auto [u, w]: G[v])
if(w < dis[u])
{
if(dis[u] != INF)
s.erase(pii(dis[u], u));
s.emplace(dis[u] = w, u);
}
}
if(left) puts("orz");
else printf("%d\n", ans);
return 0;
}
|
习题
总结
我们来看一下Kruskal、Prim两种算法的对比:
| 指标 |
Kruskal |
Prim |
| 时间复杂度 |
$\mathcal O(m\log m)$ |
$\mathcal O(n\log m)$ |
| 运行时间 |
$255\mathrm{ms}$ |
$328\mathrm{ms}$ |
| 编码难度 |
低 |
中 |
| 适用域 |
稀疏图 |
稠密图 |
由此可见,大部分题目首选Kruskal,有特殊需要时才使用Prim。
本篇文章到此结束,如果觉得好的话就请给个三连,感谢大家的支持!
