前言
在图中,如果要求任意两点间的距离,则可以使用Floyd($\mathcal O(N^3)$;))和Dijkstra($\mathcal O(NM\log M)$:))。对于比较小的数据范围(一般为顶点数$N\le 150$),可以使用Floyd算法。本文将讲述Floyd算法的原理、实现和扩展应用。
如果有哪里写得不好请各位dalao多多指教,谢谢!
原理
不同于Dijkstra,Floyd算法同样适用于带负边权的最短路问题。其原理为:
令$f(x,y)$为从顶点$x$到$y$的最短路径。初始时,有:
$$
f(x,y)=
\begin{cases}
0 & (x=y) \\
G[x][y] & (G[x][y]\ne0)\\
+\infin & (x\ne y,G[x][y]=0)
\end{cases}
$$
其中$G$为图的邻接矩阵,$G[x][y]$表示顶点$x$到$y$的边权,$0$表示$x$到$y$没有连边。
接下来,考虑枚举中间点$k$,按$x\to k\to y$的路线计算最短路,则伪代码为:
1
2
3
4
|
for k = 1, 2, ..., n
for x = 1, 2, ..., n
for y = 1, 2, ..., n
f[x][y] = min(f[x][y], f[x][k] + f[k][y])
|
此时,算法结束,最终$f(x,y)$即为从$x$到$y$的最短路。
注意:当给定图为无向图时,对于任意$(x,y)$,$G[x][y]=G[y][x]$,则$f(x,y)=f(y,x)$,可改变计算过程(如变成f[k][x]+f[k][y]);但若是有向图,请务必按照伪代码中的顺序编写程序!
代码
Floyd算法的代码可在洛谷 B3647提交。下面给出这题对应的AC代码(注意是按边输入):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <cstdio>
#include <cstring>
#define maxn 100
using namespace std;
int dis[maxn][maxn];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
// 初始化,注意初始值不能超过INT_MAX/2(防止两个INF相加溢出)
memset(dis, 0x3f, sizeof dis);
// 每个点到自己的距离为0
for(int i=0; i<n; i++)
dis[i][i] = 0;
// 读入边
while(m--)
{
int u, v, d;
scanf("%d%d%d", &u, &v, &d);
u --, v --; // 0-index
dis[u][v] = dis[v][u] = d; // 注意两个值都要设
}
// Floyd 算法流程
for(int k=0; k<n; k++) // 中间点
for(int i=0; i<n; i++) // 起始点
for(int j=0; j<n; j++) // 终点
{
int d = dis[i][k] + dis[k][j]; // i->k->j
if(d < dis[i][j]) dis[i][j] = d; // 取最短长度
}
for(int i=0; i<n; i++, putchar('\n'))
for(int j=0; j<n; j++)
printf("%d ", dis[i][j]);
return 0;
}
|
扩展
下面问题来了:如何输出结果路径?其实方法很简单。与Dijkstra类似但略有不同,设$\text{path}(x, y)=x\to y$的最短路径上的某一点,则状态转移时若$f(x,k)+f(k,y) < f(x,y)$,则不仅要更新$f(x,y)$,还要更新$\text{path}(x,y):=k$。最后,递归输出结果即可。
题面
给定一张有$N$个点,$M$条边的简单无向图,对于每一对$(i,j)$($1\le i < j\le N$),求$i\to j$的最短路径上的每一点。
样例
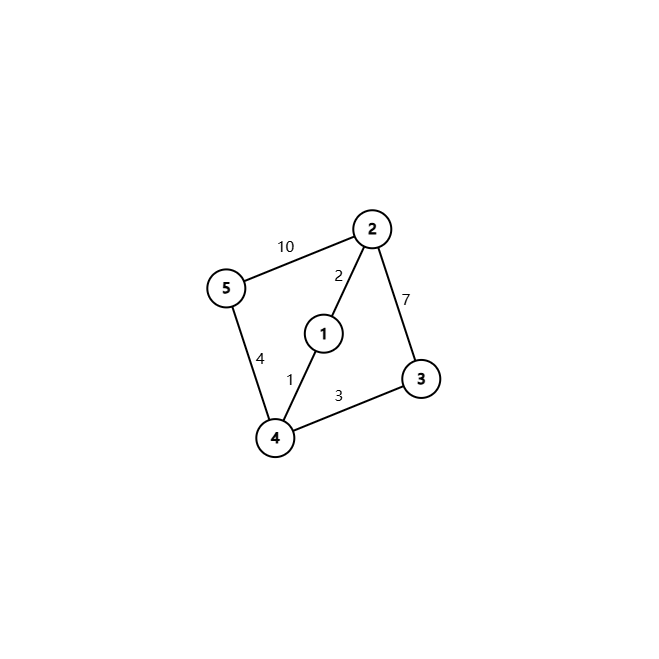
输入:
1
2
3
4
5
6
7
|
5 6
3 4 3
4 1 1
4 5 4
1 2 2
5 2 10
3 2 7
|
输出:
1
2
3
4
5
6
7
8
9
10
|
1->2: 1 2
1->3: 1 4 3
1->4: 1 4
1->5: 1 4 5
2->3: 2 1 4 3
2->4: 2 1 4
2->5: 2 1 4 5
3->4: 3 4
3->5: 3 4 5
4->5: 4 5
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
#include <cstdio>
#include <cstring>
#define maxn 100
using namespace std;
int dis[maxn][maxn], path[maxn][maxn];
void print(int x, int y) // 递归输出x->y的路径,不包含y
{
int k = path[x][y]; // x->k->y
if(k == x || k == y) // 两点相邻,直接输出
printf(" %d", x);
else
{
// 分成两部分递归
print(x, k); // x->k
print(k, y); // k->y
}
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
// 初始化
memset(dis, 0x3f, sizeof dis);
for(int i=0; i<n; i++)
dis[i][i] = 0;
// 读入边
while(m--)
{
int u, v, d;
scanf("%d%d%d", &u, &v, &d);
dis[u][v] = dis[v][u] = d; // 注意两个值都要设
path[u][v] = path[v][u] = u; // 初始化path
}
// Floyd 算法流程,为了方便输出,采用1-index
for(int k=1; k<=n; k++) // 中间点
for(int i=1; i<=n; i++) // 起始点
for(int j=1; j<=n; j++) // 终点
{
int d = dis[i][k] + dis[k][j]; // i->k->j
if(d < dis[i][j]) // 更新最短路径
dis[i][j] = d, path[i][j] = k;
}
// 依次枚举(i,j) 输出路径
for(int i=1; i<n; i++)
for(int j=i+1; j<=n; j++)
{
printf("%d->%d:", i, j);
print(i, j);
printf(" %d\n", j);
}
return 0;
}
|
注:由于每条路径的长度不会超过$N$,所以总时间复杂度仍为$\mathcal O(N^3)$。
后记
总结:Floyd算法时间复杂度为$\mathcal O(N^3)$,写起来很方便。如果觉得好就请给个三连,谢谢支持!
