【算法笔记】树状数组/Binary Indexed Tree/Fenwick Tree

前言

树状数组，即树形存储的数组，又称Binary Indexed Tree或Fenwick Tree。
抛开它树形的存储结构，这种神奇的数据结构的应用看起来与「树」没什么关系：

有一个序列$A=(A_1,A_2,\dots,A_N)$，在不超过$\mathcal O(\log N)$的时间复杂度内完成下列操作：
$\to~$求$[L,R]$区间内所有数之和。
$\to~$指定一个元素$A_x$，将其加上$k$。

如果想要使求和操作尽可能快，很容易想到前缀和，这样求和操作只要$\mathcal O(1)$的时间，但更新操作的时间复杂度就升至$\mathcal O(N)$，无法满足题目要求；反之，若直接暴力维护$A$中所有元素的值，则虽然更新操作只需要$\mathcal O(1)$，但求和操作的时间又变成了$\mathcal O(N)$，还是满足不了要求。那有没有一种算法，综合了两种方式的优势，达到题目时间要求呢？

肯定有，那就是今天说的——树状数组。

基本算法

洛谷 P3374【模板】树状数组 1
同“前言”中的部分，$1\le n,m\le 10^5$，其中$m$为操作总次数。

由于$n,m\le 10^5$，所以$\mathcal O(nm)$的暴力解法肯定行不通，需要使用$\mathcal O(M\log N)$的树状数组。其存储结构大致上是这样的：
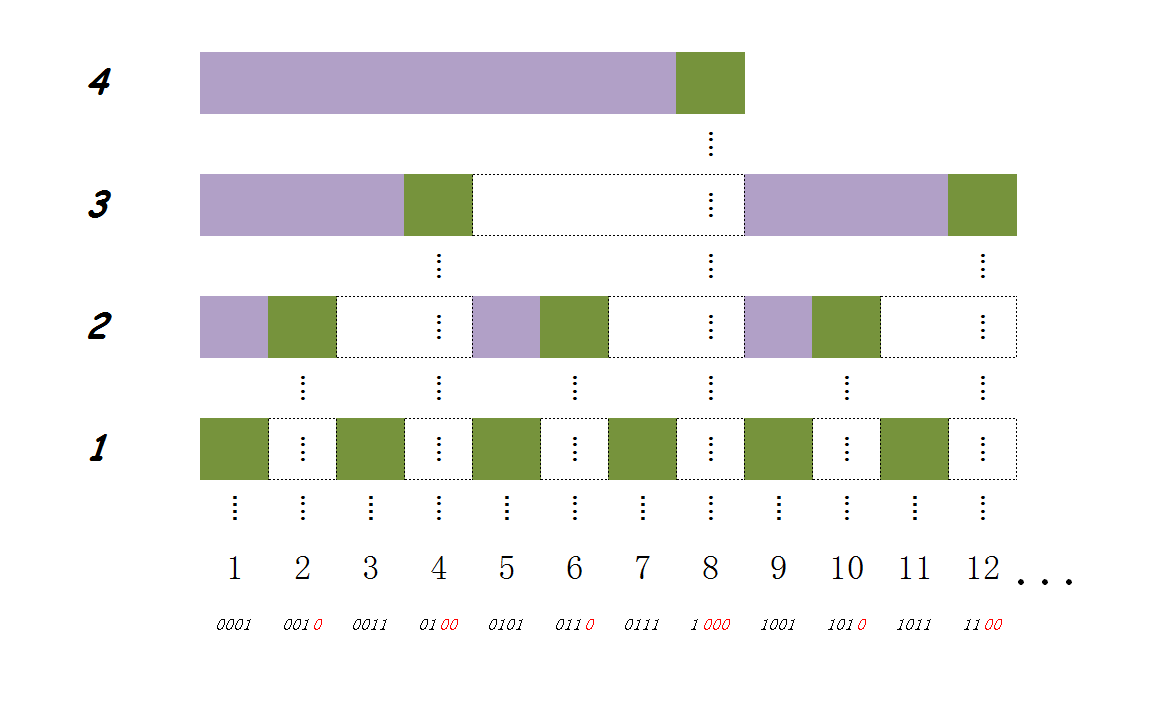
树状数组结构

是不是已经有些明白了？这里我们我们把$B$当作树状数组的内部存储，则据图可知：

$B_1=A_1$
$B_2=A_1+A_2$
$B_3=A_3$
$B_4=A_1+A_2+A_3+A_4$
$B_5=A_5$
$B_6=A_5+A_6$
$B_7=A_7$
$B_8=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8$
..

可以看出，$B_i=A_{i-2^k+1}+A_{i-2^k+2}+\dots+A_i$，其中$k$为$i$在二进制下末尾$0$的的个数。换句话说，$2^k$就是$i$在二进制中的的lowbit。

关于lowbit函数
$\to~$lowbit的定义：

$\mathrm{lowbit}(0)$ 无意义。

对于任意$x > 0$，$\mathrm{lowbit}(x)=2^k$，其中$k$为$x$在二进制下末尾$0$的的个数。

$\to~$举例：$\mathrm{lowbit}(10010)=10$；$\mathrm{lowbit}(10000)=10000$
$\to~$C/C++实现：
1
2
3
inline int lowbit(int x) {
    return x & -x;
}
或宏定义形式：
1
#define lowbit(x) (x) & -(x)

$$ l:=i-\mathrm{lowbit}(i)+1\\ r:=i\\ B_i=\sum_{j=l}^{r} A_j $$

按照这样，就可以在$\mathcal O(\log n)$的时间复杂度内求$[0,x]$中整数之和（prefixSum(x)）或将$A_x$加上$k$（update(x, k)）。
对于$[L,R]$的区间之和，可以按照segmentSum(l, r) = prefixSum(r) - prefixSum(l - 1)的方式进行计算。详见代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


#include <cstdio>
using namespace std;

template <typename value_type>
class fenwick_tree {
private:
	const int n;
	value_type* a;
	inline int lowbit(int x) { return x & -x; }
public:
	inline fenwick_tree(int m): n(m) {
		a = new value_type[n + 1];
		for(int i=0; i<=n; i++)
			a[i] = 0;
	}
	inline ~fenwick_tree() { delete[] a; }
	inline value_type prefixSum(int i) {
		value_type res = 0;
		for(; i; i-=lowbit(i)) res += a[i];
		return res;
	}
	inline value_type segmentSum(int l, int r) {
		return prefixSum(r) - prefixSum(l - 1);
	}
	inline void update(int i, const value_type& d) {
		for(; i<=n; i+=lowbit(i))
			a[i] += d;
	}
};

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	fenwick_tree<int> bit(n);
	for(int i=1; i<=n; i++)
	{
		int a;
		scanf("%d", &a);
		bit.update(i, a);
	}
	while(m--)
	{
		int op, x, y;
		scanf("%d%d%d", &op, &x, &y);
		if(op == 1) bit.update(x, y);
		else printf("%d\n", bit.segmentSum(x, y));
	}
	return 0;
}

在洛谷 P3374上提交耗时仅$572\mathrm{ms}$，同题用同样为$\mathcal O(\log N)$的线段树耗时约$2.5\mathrm{s}$，可见相比于线段树算法，使用树状数组不仅代码量小、容易实现，还有运行速度快等等优势。

基础算法到此为止，下面来看一些经典的扩展应用。

扩展应用

知识补充：离散化
对于序列$A=(A_1,A_2,\dots,A_N)$，我们将$A$中的每个数都按原先的映射到一个$[1,N]$的范围内，这个过程被称为离散化。一般来说，离散化时同样的元素映射到同样的值，不同的元素映射到不同的值，且满足原先的大小关系。换句话说，令原先的序列为$(A_1,\dots,A_N)$，离散化后的序列为$(B_1,\dots,B_N)$，则满足如下条件：

$1\le B_i\le N$（$1\le i\le N$）
若$i \ne j$，且$A_i < A_j$，则$B_i < B_j$。
若$i \ne j$，且$A_i = A_j$，则$B_i = B_j$。
若$i \ne j$，且$A_i > A_j$，则$B_i > B_j$。

求逆序对

逆序对问题是经典的序列问题。众所周知，这类问题可以用归并排序在$\mathcal O(N\log N)$的时间内解决。不过，既然今天讲的是树状数组，~~那就不能用归并排序~~，就主要来说一说树状数组的解法。

洛谷 P1908 逆序对
给定一个整数序列$A=(A_1,A_2,\dots,A_N)$，求其中逆序对的个数。
一个整数对$(i,j)$被称为“逆序对”，当且仅当如下条件满足：
$\to 1\le i < j\le N$
$\to A_i > A_j$
数据范围：$N\le 10^5,A_i\le 10^9$。

由于$N\le 10^5$，所以暴力的$\mathcal O(N^2)$做法肯定不行。
我们考虑使用树状数组，先将数组离散化成$[1,N]$之间的数，记离散化后的序列为$B=(B_1,\dots,B_N)$。我们按$($总数对数量$)-($非逆序对数量$)=($逆序对数量$)$的公式计算，其中总数对的数量为$1+2+\dots+N-1=\frac {N(N-1)}2$。用树状数组维护每个数字的出现次数，则非逆序对的数量可以在遍历$B$中的每个元素时动态计算。详见代码。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58


#include <cstdio>
#include <algorithm>
#define maxn 500005
using namespace std;

inline int read() {
	static char c;
	while((c = getchar()) < '0' && c > '9');
	int res = c ^ 48;
	while((c = getchar()) >= '0' && c <= '9')
		res = (res << 3) + (res << 1) + (c ^ 48);
	return res;
}

template <typename value_type>
class fenwick_tree {
private:
	const int n;
	value_type* a;
	inline int lowbit(int x) { return x & -x; }
public:
	inline fenwick_tree(int m): n(m) {
		a = new value_type[n + 1];
		for(int i=0; i<=n; i++)
			a[i] = 0;
	}
	inline ~fenwick_tree() { delete[] a; }
	inline value_type prefixSum(int i) {
		value_type res = 0;
		for(++i; i; i-=lowbit(i)) res += a[i];
		return res;
	}
	inline void update(int i, const value_type& d) {
		for(++i; i<=n; i+=lowbit(i))
			a[i] += d;
	}
};

int a[maxn], rk[maxn];

int main()
{
	int n = read();
	for(int i=0; i<n; i++)
		a[rk[i] = i] = read();
	stable_sort(rk, rk + n, [&](int x, int y) -> bool {
		return a[x] < a[y];
	}); // 因为可能会有重复的数字，所以必须使用稳定的stable_sort排序，用sort只有40分
	fenwick_tree<int> bit(n); // 初始化树状数组，离散化之后大小为n就行
	long long ans = n * (n - 1LL) >> 1LL; // 总数对个数
	for(int i=0; i<n; i++)
	{
		ans -= bit.prefixSum(rk[i]); // 减去非逆序数对，即prefixSum(b[i])
		bit.update(rk[i], 1); // 动态更新当前元素出现次数
	}
	printf("%lld\n", ans);
	return 0;
}

习题：CF1676H2 Maximum Crossings (Hard Version)

区间更新

用过线段树的都知道，树状数组最大的缺点就是无法直接实现区间更新。不过，在一些特殊情况¹下，我们可以通过差分+离散化来间接实现区间的更新。先来看洛谷上的模板：

P3368【模板】树状数组 2
已知一个长为$N$的数列，你需要进行下面两种操作：

1 x y k：将$[x,y]$区间内的每个数都加上$k$。

2 x：求第$x$个数的值。

运用差分的思想，用树状数组维护$A$的差分数组$B$（$B_i=A_i-A_{i-1}$）。
此时，我们可以把“区间$[x,y]$中所有元素都加上$k$”看作：

$B_x:=B_x+k$
$B_{y+1}:=B_{y+1}-k$

此时，$A_x=B_1+\dots+B_x$，正好是树状数组的前缀和操作。
于是，我们在$\mathcal O(N\log N)$的时间复杂度内解决了这个问题。

C++实现如下（此实现方式与前面讲的略有不同）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#include <cstdio>
#define maxn 500005
using namespace std;

template <typename value_type>
class fenwick_tree {
private:
	const int n;
	value_type* a;
	inline int lowbit(int x) { return x & -x; }
public:
	inline fenwick_tree(int m): n(m) {
		a = new value_type[n + 1];
		for(int i=0; i<=n; i++)
			a[i] = 0;
	}
	inline ~fenwick_tree() { delete[] a; }
	inline value_type prefixSum(int i) {
		value_type res = 0;
		for(; i; i-=lowbit(i)) res += a[i];
		return res;
	}
	inline void update(int i, const value_type& d) {
		for(; i<=n; i+=lowbit(i))
			a[i] += d;
	}
};

int a[maxn];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=n; i++)
		scanf("%d", a + i);
	fenwick_tree<int> bit(n);
	while(m--)
	{
		int op;
		scanf("%d", &op);
		if(op == 1)
		{
			int l, r, k;
			scanf("%d%d%d", &l, &r, &k);
			bit.update(l, k);
			if(r < n) bit.update(r + 1, -k);
		}
		else
		{
			int x;
			scanf("%d", &x);
			printf("%d\n", a[x] + bit.prefixSum(x));
		}
	}
	return 0;
}

习题

洛谷 P1168 中位数（求第$k$大问题）
洛谷 P1637 三元上升子序列
洛谷 P6477 [NOI Online #2 提高组] 子序列问题
洛谷 P8253 [NOI Online 2022 提高组] 如何正确地排序
AtCoder Beginner Contest 256 F - Cumulative Cumulative Cumulative Sum
P3372【模板】线段树 1（没错，就是线段树模板，不妨考虑一下「超级树状数组」？）

总结

树状数组支持更新、求和两种操作。欢迎大家前来提问或补充~
~~求三连qwq~~

实际上所有情况都可以，不过其他的非特殊情况实现起来非常繁琐，有时还不如直接用线段树来得方便，因此这里忽略这种情况。 ↩︎