AtCoder Beginner Contest 252 A~G 题解

前言

  • 这是我第一次写7题（A~G）的ABC题解，若有写得不好或者不到位的地方请多多指教，我将万分感激，感谢大家的支持！

A - ASCII code

题目大意

给定正整数$N$，输出ASCII码是$N$的字母。
$97\le N\le 122$

输入格式

$N$

输出格式

输出ASCII码是$N$的字母。

分析

注意a对应$97$，b对应$98$，……，z对应$122$。
安上小白专属转换教程：

  • C 
    1
2

    int n = 97;
putchar(n); /* 输出：a */
    putchar函数自动转换为字符，也可以使用printf("%c", n)效果相同
  • C++ 
    1
2

    int n = 97;
cout << char(n) << endl; // 输出：a
    直接cout << n会输出97，需要用char转换为字符
  • Python 
    1
2

    n = 97
print(chr(n)) # 输出：a
    同样也不能直接输出，需要用chr转换
  • Java 
    1
2
3

    int n = 97;
char c = (char) n;
System.out.print(c);
    与C++、Python类似，需要转换
  • JavaScript 
    1
2
3

    var n = 97;
var c = String.fromCharCode(n);
console.log(c); // 输出：a
    同样使用接口转化，需调用String.fromCharCode

再不懂你试试……

代码

太水，直接走一发py（现场25秒AC）

1

print(chr(int(input())))

B - Takahashi’s Failure

题目大意

Takahashi的房子里有$N$个食物。第$i$个食物的美味度是$A_i$。
其中，他不喜欢$K$个食物：$B_1,B_2,\dots,B_K$。
已知Takahashi会从$N$个食物中随机选取一个美味度最大的食物，并把它吃掉。
Takahashi是否有可能迟到不喜欢的食物？

$1\le K\le N\le 100$
$1\le A_i\le 100$
$1\le B_i\le N$

输入格式

$N~K$
$A_1~\dots~A_N$
$B_1~\dots~B_K$

输出格式

如果有可能，输出Yes；否则，输出No。

分析

只要有不喜欢的食物美味度最高就有可能，否则不可能。详见代码。

代码

还是水，注意如果是$\text{0-indexed}$的话$B_i$要减$1$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <cstdio>
using namespace std;

int a[105];

int main()
{
	int n, k, mx = 0;
	scanf("%d%d", &n, &k);
	for(int i=0; i<n; i++)
	{
		scanf("%d", a + i);
		if(a[i] > mx) mx = a[i];
	}
	while(k--)
	{
		scanf("%d", &n);
		if(a[--n] == mx)
		{
			puts("Yes");
			return 0;
		}
	}
	puts("No");
	return 0;
}

C - Slot Strategy

题目大意

略，请自行前往AtCoder查看。

$2\le N\le 100$

输入格式

$N$
$S_1$
$\vdots$
$S_N$

输出格式

输出答案。

分析

令$\text{cnt}[i][j]=(S_k[j]=i$的个数$)$，对最终变成$0$-$9$分别计算代价即可。详见代码。

代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <cstdio>
using namespace std;

int cnt[10][10]; // cnt[i][j] = number of (s[j]=i)

int main()
{
	int n;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
	{
		char s[15];
		scanf("%s", s);
		for(int j=0; j<10; j++)
			cnt[s[j] ^ 48][j] ++;
	}
	int ans = 1000;
	for(int i=0; i<10; i++)
	{
		int cur = 0;
		for(int j=0; j<10; j++)
		{
			int c = j + (cnt[i][j] - 1) * 10;
			if(c > cur) cur = c;
		}
		if(cur < ans) ans = cur;
	}
	printf("%d\n", ans);
	return 0;
}

D - Distinct Trio

题目大意

给定长为$N$的整数序列$A=(A_1,\dots,A_N)$。
求符合以下条件的整数对$(i,j,k)$的个数：

  • $1\le i < j < k\le N$
  • $A_i\ne A_j\ne A_k$

$3\le N\le 2\times 10^5$
$1\le A_i\le 2\times 10^5$

输入格式

$N$
$A_1~\dots~A_N$

输出格式

输出一行，即符合条件的整数对$(i,j,k)$的个数。

分析

本题主要有两种思路：

  1. 逆向思维，用总数-不符合条件的；
  2. 将题目转化为求$A_i < A_j < A_k$的$(i,j,k)$的个数。

这里介绍第一种方法（第二种方法较为简单，不详细说明）。

首先易得，总共的$1\le i < j < k\le N$有$C_n^3$种取法。
然后考虑$A_i,A_j,A_k$中有重复的个数：

  • 对于$A$中每个数$x$，我们记录$\text{cnt}_x=A$中$x$出现的次数；
  • 然后，如果$\text{cnt}_x\ge 2$，则将答案减去$C_{\text{cnt}_x}^2\times(N-\text{cnt}_x)$，即$x,x,y$格式出现的次数；
  • 又如果$\text{cnt}_x\ge 3$，将答案减去$C_{\text{cnt}_x}^3$，即$x,x,x$的次数。

总时间复杂度为$\mathcal O(N+\max_A-\min_A)$，空间复杂度为$\mathcal O(\max_A-\min_A)$。

代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <cstdio>
#define maxn 200005
using namespace std;

using LL = long long;
int cnt[maxn];

inline LL C2(int n) { return n * (n - 1LL) >> 1LL; }
inline LL C3(int n) { return C2(n) * (n - 2LL) / 3LL; }

int main()
{
	int n;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
	{
		int a;
		scanf("%d", &a);
		cnt[a] ++;
	}
	LL ans = C3(n);
	for(int i=1; i<maxn; i++)
		if(cnt[i] > 1)
		{
			ans -= C2(cnt[i]) * (n - cnt[i]);
			if(cnt[i] > 2) ans -= C3(cnt[i]);
		}
	printf("%lld\n", ans);
	return 0;
}

E - Road Reduction

题目大意

给定一张由$N$个点和$M$条边组成的简单无向图。
第$i$条边长度为$C_i$，同时连接点$A_i$和$B_i$。
求任意一颗生成树，使得从点$1$到其他所有点的距离之和最小。

$2\le N\le 2\times 10^5$
$N-1\le M\le 2\times 10^5$
$1\le A_i < B_i\le N$
$(A_i,B_i)\ne(A_j,B_j)$（$i\ne j$）
$1\le C_i\le 10^9$

输入格式

$N~M$
$A_1~B_1~C_1$
$\vdots$
$A_M~B_M~C_M$

输出格式

按任意顺序输出留下来的$N-1$条边的下标，用空格隔开。

分析

显然，在生成树中，点$1$到任意点的距离肯定不少于在原图中到这个点的距离。
因此，如果两个距离相等，显然就是最优解。
此时可以证明，肯定有这样的解。使用Dijkstra算法求最短路径的同时，记录到每个点之前的最后一条路即可。

代码

Dijkstra的两种经典实现方式，$\mathcal O(N\log N+M\log N)$

  • priority_queue优先队列（$182\text{ms}$） 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

    #include <cstdio>
#include <queue>
#define maxn 200005
#define INF 9223372036854775807LL
using namespace std;

using LL = long long;
using pli = pair<LL, int>;

struct Edge
{
	int v, id; LL d;
	inline Edge(int u, int l, int i): v(u), d(l), id(i) {}
};

vector<Edge> G[maxn];
LL dis[maxn];
int ans[maxn];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		G[--a].emplace_back(--b, c, i);
		G[b].emplace_back(a, c, i);
	}
	priority_queue<pli, vector<pli>, greater<pli>> q;
	for(int i=1; i<n; i++) dis[i] = INF;
	q.emplace(0LL, 0);
	while(!q.empty())
	{
		auto [d, v] = q.top(); q.pop();
		if(dis[v] == d)
			for(const Edge& e: G[v])
			{
				LL nd = d + e.d;
				if(nd < dis[e.v])
					q.emplace(dis[e.v] = nd, e.v),
					ans[e.v] = e.id;
			}
	}
	for(int i=1; i<n; i++) printf("%d ", ans[i]);
	return 0;
}
  • set集合（$202\text{ms}$） 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

    #include <cstdio>
#include <vector>
#include <set>
#define maxn 200005
#define INF 9223372036854775807LL
using namespace std;

using LL = long long;
using pli = pair<LL, int>;

struct Edge
{
	int v, id; LL d;
	inline Edge(int u, int l, int i): v(u), d(l), id(i) {}
};

vector<Edge> G[maxn];
LL dis[maxn];
int ans[maxn];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		G[--a].emplace_back(--b, c, i);
		G[b].emplace_back(a, c, i);
	}
	set<pli> s; // <distance, vertex>
	for(int i=1; i<n; i++) dis[i] = INF;
	s.emplace(0LL, 0);
	while(!s.empty())
	{
		auto [d, v] = *s.begin(); s.erase(s.begin());
		for(const Edge& e: G[v])
		{
			LL nd = d + e.d;
			if(nd < dis[e.v])
			{
				if(dis[e.v] < INF)
					s.erase(pli(dis[e.v], e.v));
				s.emplace(dis[e.v] = nd, e.v);
				ans[e.v] = e.id;
			}
		}
	}
	for(int i=1; i<n; i++) printf("%d ", ans[i]);
	return 0;
}

注意使用long long。

F - Bread

题目大意

本题翻译已经过简化，部分表示与原题不同，仅供参考，请以原题为准。

有一个的整数序列$S$，初始只有一个元素$L$，我们可以执行如下操作无限次：

  • 从$S$中删去任意元素$k$（$k > 1$），同时选取整数$x$（$1\le x\le k-1$），将$x$和$k-x$放入$S$。此操作的代价为$k$。

求最小的代价，使得$A$在$S$中，即$A$中每个元素的出现次数$~\le S$中对应元素的出现次数。

$2\le N\le 2\times 10^5$
$1\le N\le 10^9$
$A_1+A_2+\dots+A_N\le L\le 10^{15}$

输入格式

$N~L$
$A_1~\dots~A_N$

输出格式

输出最小的代价。

分析

本题考虑逆向思维，仔细思考后发现题目可以如下转化：

  • 令$S=(A_1,\dots,A_N,L-\sum A)$（$L=\sum A$时不千万不要加上最后一个元素）
  • 每次操作将$A$中任意两个元素合并，它们的和即为合并后新的元素，也是本次操作的代价
  • 最后发现全部合并完后$S$中正好剩下一个$L$，此时操作结束，所有代价和即为方案的最终代价。

此时，显然每次合并最小的两个数即为最优方案，因此可以使用优先队列实现，总时间复杂度为$\mathcal O(N\log N)$。

代码

注意使用long long。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <cstdio>
#include <queue>
using namespace std;

using LL = long long;

int main()
{
	int n;
	LL l;
	scanf("%d%lld", &n, &l);
	priority_queue<LL, vector<LL>, greater<LL>> q;
	for(int i=0; i<n; i++)
	{
		int x;
		scanf("%d", &x);
		q.push(x);
		l -= x;
	}
	if(l > 0) q.push(l);
	LL ans = 0LL;
	while(q.size() > 1)
	{
		LL x = q.top(); q.pop();
		x += q.top(); q.pop();
		ans += x;
		q.push(x);
	}
	printf("%lld\n", ans);
	return 0;
}

G - Pre-Order

题目大意

有一颗由$N$个节点$1,2,\dots,N$组成的树，它的根节点为$1$。
它的先序遍历序列是$(P_1,P_2,\dots,P_N)$。
每次搜索时，我们都会优先前往编号小的节点。
有多少种不同的树，使其符合上述条件？对$998244353$取模。

$2\le N\le 500$
$1\le P_i\le N$
$P_1=1$
$P_1\ne P_2\ne\dots\ne P_N$

输入格式

$N$
$P_1~\dots~P_N$

输出格式

输出答案，对$998244353$取模。

分析

我们先将$P$变为$\text{0-indexed}$，即原来的$(P_1,P_2,\dots,P_N)$分别对应$(A_0,A_1,\dots,A_{N-1})$。
此时，不妨考虑区间$\text{dp}$的思想，设$\mathrm{dp}(l,r)=~($一棵树已经去掉根节点的先序遍历为$A_l,A_{l+1},\dots,A_{r-1}$的可能数$)$，则$\mathrm{dp}(1,N)$即为所求。

下面考虑$\mathrm{dp}(l,r)$的动态转移方程。

  • 先考虑$A_l$为$A_{l+1},\dots,A_{r-1}$的祖宗的情况，如图：
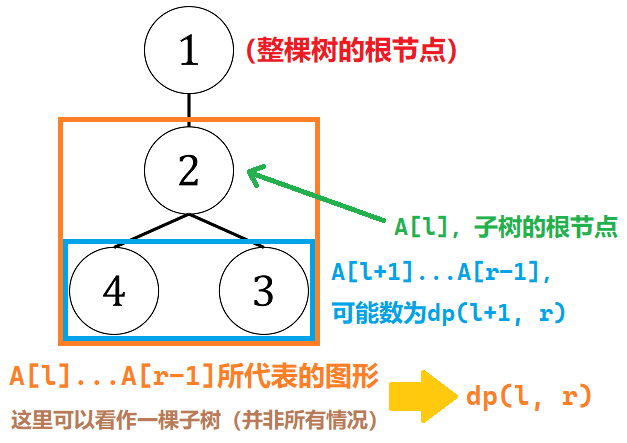
    情况一示意图

易得，此时$\mathrm{dp}(l,r)$初始化为$\mathrm{dp}(l+1,r)$。

  • 再考虑区分左右子树，对于每个$k$（$l < k < r$），将$A_l,\dots,A_{k-1}$当作左子树（可能数为$\mathrm{dp}(l+1,k)$），再将$A_k,\dots,A_{r-1}$当作右子树（可能数为$\mathrm{dp}(k,r)$），此时如果$A_l < A_k$则符合题意，将$\mathrm{dp}(l,r)$加上$\mathrm{dp}(l+1,k)\times \mathrm{dp}(k,r)$即可。

至此，本题已结束，时间复杂度为$\mathcal O(N^3)$。

代码

注意事项：

  1. 乘法操作需要转为long long再取模。
  2. 答案为$\mathrm{dp}(1,N)$，不是$\mathrm{dp}(0,N)$。
  3. 注意区间$\text{dp}$计算顺序，参考代码提供两种写法（先枚举$l$和先枚举长度）。
  • 写法一（先枚举$l$，$59\text{ms}$） 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

    #include <cstdio>
#define MOD 998244353
#define maxn 505
using namespace std;

using LL = long long;
int p[maxn], dp[maxn][maxn];

int main()
{
	int n;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
		scanf("%d", p + i);
	for(int l=n; l>0; l--)
	{
		dp[l][l] = 1;
		for(int r=l+1; r<=n; r++)
		{
			dp[l][r] = dp[l + 1][r];
			for(int k=l+1; k<r; k++)
				if(p[l] < p[k] && (dp[l][r] += LL(dp[l + 1][k]) * dp[k][r] % MOD) >= MOD)
					dp[l][r] -= MOD;
		}
	}
	printf("%d\n", dp[1][n]);
	return 0;
}
  • 写法二（先枚举长度，$66\text{ms}$） 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

    #include <cstdio>
#define MOD 998244353
#define maxn 505
using namespace std;

using LL = long long;
int p[maxn], dp[maxn][maxn];

int main()
{
	int n;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
		scanf("%d", p + i);
	for(int i=1; i<=n; i++)
		dp[i][i] = 1;
	for(int d=1; d<=n; d++)
		for(int l=1, r=d+1; r<=n; l++, r++)
		{
			dp[l][r] = dp[l + 1][r];
			for(int k=l+1; k<r; k++)
				if(p[l] < p[k] && (dp[l][r] += LL(dp[l + 1][k]) * dp[k][r] % MOD) >= MOD)
					dp[l][r] -= MOD;
		}
	printf("%d\n", dp[1][n]);
	return 0;
}
© 2020 - 2025 GoodCoder's Blog
使用 Hugo 构建
主题 Stack 由 Jimmy 设计