C - Knight Fork

题目大意

在二维平面上是否有一个整数坐标点到$(x_1,y_1)$和$(x_2,y_2)$的欧几里得距离都是$\sqrt5$？

输入格式

$x_1~y_1~x_2~y_2$

输出格式

如果存在符合条件的点，输出Yes；否则，输出No。

样例

$x_1$	$y_1$	$x_2$	$y_2$	输出
$0$	$0$	$3$	$3$	`Yes`
$0$	$1$	$2$	$3$	`No`
$1000000000$	$1000000000$	$999999999$	$999999999$	`Yes`

分析

$$ (a-c)^2+(b-d)^2=5\\ \{a-c,b-d\}=\{1,2\} $$

所以，对于$(0,0)$这个点，有如下距离为$\sqrt5$的点（其他点都类似）：
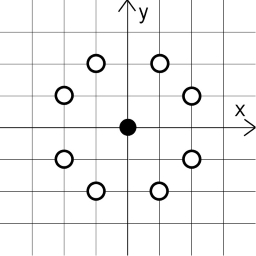
距离sqrt5解释图

所以，我们对找到$(x_1,y_1)$所有的距离为$\sqrt5$的点，并对计算与$(x_2,y_2)$的距离即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


#include <cstdio>
using namespace std;

using LL = long long;
const int d[8] = {-1, 1, 2, 2, 1, -1, -2, -2};

inline LL sqr2(const LL& x, const LL& y)
{
	return x * x + y * y;
}

int main()
{
	LL x1, y1, x2, y2;
	scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2);
	x1 -= x2, y1 -= y2;
	for(int i=0; i<8; i++)
		if(sqr2(x1 + d[i], y1 + d[(i + 2) & 7]) == 5)
		{
			puts("Yes");
			return 0;
		}
	puts("No");
	return 0;
}

D - Prime Sum Game

~~==水题警告==~~

题目大意

Takahashi和Aoki在玩一个游戏。游戏过程如下：

Takahashi在中选择一个整数$A\le N\le B$。
Aoki中选择一个整数$C\le M\le D$。
如果$N+M$是质数，Aoki获胜。否则，Takahashi获胜。

当两人都按最优策略游戏时，谁会赢得比赛？

$1\le A\le B\le 100$
$1\le C\le D\le 100$

输入格式

$A~B~C~D$

输出格式

输出胜者的名字，即Takahashi或Aoki。

样例

$A$	$B$	$C$	$D$	输出
$2$	$3$	$3$	$4$	`Aoki`
$1$	$100$	$50$	$60$	`Takahashi`
$3$	$14$	$1$	$5$	`Aoki`

分析

要解决这道题，首先要知道什么是“最优策略”。
显然，当Takahashi选择的$N$加上任意的$M$都不是质数时，Takahashi胜利；
否则，当任意的$N$加上某一个$M$都得到质数时，Aoki胜利。
因为数据范围较小，我们可以暴力枚举所有$N$和$M$，质数判断耗时可以忽略不计。因此，总时间复杂度约为$\mathcal O(BD)$。

代码

P.S. 不可思议，运行时间居然是$4\mathrm{ms}$..（本来以为至少也有$30\mathrm{ms}$的..）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


#include <cstdio>
using namespace std;

inline bool isprime(int x)
{
	for(int t=__builtin_sqrt(x), i=2; i<=t; i++)
		if(x % i == 0)
			return false;
	return true;
}

int main()
{
	int a, b, c, d;
	scanf("%d%d%d%d", &a, &b, &c, &d);
	for(int i=a; i<=b; i++)
	{
		int j = c;
		for(; j<=d; j++)
			if(isprime(i + j))
				break;
		if(j > d) { puts("Takahashi"); return 0; }
	}
	puts("Aoki");
	return 0;
}

E - Subtree K-th Max

题目大意

有一个由$N$个节点（节点$1$，..，节点$N$）组成的树（根节点为节点$1$）。
第$i$条边连接节点$A_i$和$B_i$。节点$v$有一个数值$X_v$。
给定$Q$个询问，第$i$个询问由$(V_i,K_i)$组成：

在以节点$V_i$为根的子树当中，求所有节点的数值的第$K$大值（不去重）。

$2\le N,Q\le 10^5$
$0\le X_i\le 10^9$
$1\le A_i,B_i,V_i\le N$
==$1\le K_i\le 20$==

输入格式

$N~Q$
$X_1~\dots~X_N$
$A_1~B_1$
$\vdots$
$A_{N-1}~B_{N-1}$
$V_1~K_1$
$\vdots$
$V_Q~K_Q$

输出格式

输出$Q$行。第$i$行应包含对第$i$个询问的回答。

样例

略，请自行前往AtCoder查看

分析

我们首先发现题面中，$1\le K\le 20$。于是我们对每个节点分别存储以它为根的子树中前$20$的数值。
于是，我们按照拓扑序（或直接$\text{DFS}$），执行如下操作：

对于叶子节点，我们只存储一个当前的数值。
对于其他的节点，先排序当前节点数值和所有孩子的前$20$，排序后取前$20$即可。

排序建议用priority_queue，时间复杂度$\mathcal O(N+Q)$或$\mathcal O(N\log N+Q)$（直接排序）。

代码

示例代码实现方式为DFS + priority_queue，用时$190\mathrm{ms}$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52


#include <cstdio>
#include <queue>
#define maxn 100005
using namespace std;

int x[maxn];
vector<int> G[maxn], dp[maxn];

void dfs(int v, int par)
{
	priority_queue<int, vector<int>, greater<int>> q;
	q.push(x[v]);
	for(int u: G[v])
		if(u != par)
		{
			dfs(u, v);
			for(int val: dp[u])
			{
				q.push(val);
				if(q.size() > 20) q.pop();
			}
		}
	while(!q.empty())
	{
		dp[v].push_back(q.top());
		q.pop();
	}
}

int main()
{
	int n, q;
	scanf("%d%d", &n, &q);
	for(int i=0; i<n; i++)
		scanf("%d", x + i);
	for(int i=1; i<n; i++)
	{
		int a, b;
		scanf("%d%d", &a, &b);
		G[--a].push_back(--b);
		G[b].push_back(a);
	}
	dfs(0, -1);
	while(q--)
	{
		int v, k;
		scanf("%d%d", &v, &k);
		const auto& d = dp[--v];
		printf("%d\n", d[d.size() - k]);
	}
	return 0;
}