A - kcal

题目大意

我们有一种每$100$毫升含有$A$千卡热量的饮料。$B$毫升的这种饮料含有多少千卡热量？

$0\le A, B\le 1000$

输入格式

$A~B$

输出格式

输出$B$毫升这种饮料包含的的千卡数。最大允许浮点数精度误差$10^{-6}$。

样例

分析

废话不多说，答案就是$\frac{AB}{100}$~

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

#include <cstdio>
using namespace std;

int main()
{
	int a, b;
	scanf("%d%d", &a, &b);
	a *= b;
	printf("%d.%d\n", a / 100, a % 100);
	return 0;
}

B - Permutation Check

题目大意

给定长度为$N$的序列$A=(A_1,A_2,\dots,A_N)$。
判断$A$是否为$(1,2,\dots,N)$的一种排列。

$1\le A_i\le N\le 10^3$

输入格式

$N$
$A_1~A_2~\dots~A_N$

输出格式

如果$A$是$(1,2,\dots,N)$的一种排列，输出Yes；否则，输出No。

样例

样例输入1

1
2

5
3 1 2 4 5

样例输出1

1

Yes

$(3,1,2,4,5)$是$(1,2,3,4,5)$的一种排列，所以我们输出Yes。

样例输入2

1
2

6
3 1 4 1 5 2

样例输出2

1

No

$(3,1,4,1,5,2)$不是$(1,2,3,4,5,6)$的一种排列，所以我们输出No。

样例输入3

1
2

3
1 2 3

样例输出3

1

Yes

样例输入4

1
2

1
1

样例输出4

1

Yes

分析

由于题目保证$1\le A_i\le N$，所以$(1,2,\dots,N)$的一种排列$A$定义如下：

• $A$中$1$到$N$每个数字不重复出现。

因此，我们可以用数组记录每个数字是否出现，所以总时间复杂度为$\mathcal O(n)$。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include <cstdio>
#define maxn 1005
using namespace std;

bool used[maxn];

int main()
{
	int n;
	scanf("%d", &n);
	for(int i=0; i<n; i++)
	{
		int a;
		scanf("%d", &a);
		if(used[a])
		{
			puts("No");
			return 0;
		}
		used[a] = true;
	}
	puts("Yes");
	return 0;
}

C - POW

题目大意

给定三个整数$A,B,C$，判断$A^C$和$B^C$哪个更大。

$-10^9\le A,B\le 10^9$
$1\le C\le 10^9$

输入格式

$A~B~C$

输出格式

本题分如下三种情况输出：

• 如果$A^C < B^C$，输出<；
• 如果$A^C > B^C$，输出>；
• 如果$A^C = B^C$，输出=。

样例

分析

首先，由于负负得正，$(-a)^2=a^2$。
这样，我们可以根据奇偶性得出，如果$n$为偶数，$(-a)^n=a^n$；但如果$n$为奇数，则$(-a)^n=-(a^n)$。
因此，我们只需判断如果$C$为偶数，将$A$替换为$|A|$，再将$B$替换为$|B|$。
最后，$A$和$B$的大小关系就是$A^C$和$B^C$的大小关系。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

#include <cstdio>
using namespace std;

int main()
{
	int a, b, c;
	scanf("%d%d%d", &a, &b, &c);
	if(!(c & 1))
	{
		if(a < 0) a = -a;
		if(b < 0) b = -b;
	}
	puts(a < b? "<": a > b? ">": "=");
	return 0;
}

D - Kth Excluded

题目大意

给定长度为$N$的正整数序列$A=(A_1,A_2,\dots,A_N)$和$Q$次查询。
在第$i$次查询中，给定正整数$K_i$，求第$K_i$小的不在$A$中的正整数。

$1\le N,Q\le 10^5$
$1\le A_1 < A_2 < \dots < A_N\le10^{18}$
$1\le K_i\le 10^{18}$

输入格式

$N~Q$
$A_1~A_2~\dots~A_N$
$K_1$
$K_2$
$\hspace{5pt}\vdots$
$K_N$

输出格式

输出$Q$行。第$i$行应该包含第$K_i$小的不在$A$中的正整数。

样例

样例输入1

1
2
3
4
5

4 3
3 5 6 7
2
5
3

样例输出1

1
2
3

2
9
4

不在$A$中的正整数有$1,2,4,8,9,10,11,\dots$，其中有：

• 第$2$小的$2$；
• 第$5$小的$9$；
• 第$3$小的$4$。

因此，我们应该依次输出2，9，4。

样例输入2

1
2
3
4

5 2
1 2 3 4 5
1
10

样例输出2

1
2

6
15

分析

本题我们可以先预处理出$A$中每个元素比它小的元素的数量，再二分查找即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include <cstdio>
#include <algorithm>
#define maxn 100005
using namespace std;

using LL = long long;
LL a[maxn];

int main()
{
	int n, q;
	scanf("%d%d", &n, &q);
	for(int i=0; i<n; i++)
	{
		scanf("%lld", a + i);
		a[i] -= i;
	}
	while(q--)
	{
		LL k;
		scanf("%lld", &k);
		printf("%lld\n", k + (upper_bound(a, a + n, k) - a));
	}
	return 0;
}

E - White and Black Balls

题目大意

有多少种排列$N$个白球和$M$个黑球的方法使得下列条件成立？

• 对于每个$i$ ($1\le i\le N+M$)，设$w_i$和$b_i$分别是最左边$i$个球中白球和黑球的数量，$w_i\le b_i+K$成立。

答案对$(10^9+7)$取模。

$0\le N,M\le10^6$
$1\le N+M$
$0\le K\le N$

输入格式

$N~M~K$

输出格式

输出答案，对$(10^9+7)$取模。

样例

分析

首先，本题中合法排列数就是如下符合任意$y\le x+K$的$(0,0)\to(M,N)$的最短路径的数量：

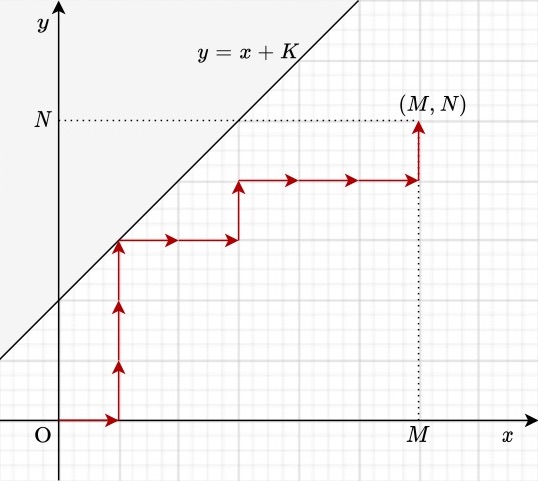
由此可见，如果$N > M+K$（即终点超出限制），答案一定为$0$。
我们还可以发现，如果没有$y\le x+K$这个限制，答案为$\binom{N + M}{N}$。
我们再考虑不合法的路径数，数量为$\binom{N + M}{M + K + 1}$。
因此，答案为$\binom{N + M}{N}-\binom{N + M}{M + K + 1}$。

代码

这里用AtCoder Library好像比较方便唉~

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include <iostream>
#include <atcoder/modint>
using namespace std;

using modint = atcoder::modint1000000007;

modint f(int n, int m)
{
	if(n < 0 || m < 0)
		return 0;
	modint ret = 1;
	for(int i=1; i<=m; i++)
		ret = ret * (n + i) / i;
	return ret;
}

int main()
{
	int n, m, k;
	scanf("%d%d%d", &n, &m, &k);
	if(n > m + k) puts("0");
	else printf("%d\n", (f(n, m) - f(n - k - 1, m + k + 1)).val());
	return 0;
}