A - Three Dice

一个人抛了三个骰子，它们的顶面分别是$a,b,c$。求它们的底面之和。
这里用的骰子是标准骰子，即两个相对的面之和为$7$。

$1\le a,b,c\le 6$

输入格式

$a~b~c$

输出格式

输出答案。

样例

$a$	$b$	$c$	答案
$1$	$4$	$3$	$13$
$5$	$6$	$4$	$6$

分析

因为两个相对的面之和为$7$，所以本题的答案为$(7-a)+(7-b)+(7-c)=21-a-b-c$。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#include <cstdio>
using namespace std;

int main()
{
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    printf("%d\n", 21 - a - b - c);
    return 0;
}

B - 180°

给定一个由0、1、6、8、9组成的字符串$S$。将其旋转$180\degree$并输出。

一个字符串旋转$180\degree$的方法：

将其翻转（reverse）。

将其中的6替换为9，9替换为6。

$1\le |S|\le10^5$

输入格式

$S$

输出格式

输出$S$旋转$180\degree$后的字符串。

样例

$S$	输出
`0601889`	`6881090`
`86910`	`01698`
`01010`	`01010`

分析

本题直接按要求模拟即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


#include <cstdio>
#define maxn 100005
using namespace std;

char s[maxn];

int main()
{
    int n = 0;
    char c;
    while((c = getchar()) != '\n')
        s[n++] = c;
    while(n--)
        putchar(s[n] == '6'? '9': s[n] == '9'? '6': s[n]);
    putchar('\n');
    return 0;
}

C - Made Up

给定三个长度为$N$的序列：$A,B,C$。
有多少对$(i,j)$符合$A_i=B_{C_j}$？

$1\le N\le 10^5$
$1\le A_i,B_i,C_i\le N$

输入格式

$N$
$A_1~A_2~\dots~A_N$
$B_1~B_2~\dots~B_N$
$C_1~C_2~\dots~C_N$

输出格式

输出符合$A_i=B_{C_j}$的$(i,j)$的对数。

样例

样例输入1

样例输出1

1

4

$4$对$(i,j)$符合条件：$(1,1),(1,3),(2,2),(3,2)$。

样例输入2

样例输出2

1

16

所有$(i,j)$都符合条件。

样例输入3

样例输出3

1

0

没有$(i,j)$符合条件。

分析

我们很容易想到$O(n^2)$的算法：暴力枚举所有$(i,j)$，并统计符合条件的对数。
可惜，这样会TLE。
我们考虑将所有的$A_i$和$B_{C_j}$分别放入两个桶$\mathrm{acnt}$和$\mathrm{bcnt}$。
根据乘法原理我们得出答案为$\sum\limits_{i=1}^n\mathrm{acnt}_i\mathrm{bcnt}_i$。

代码

注意：不要忘记使用long long！

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


#include <cstdio>
#define maxn 100005
using namespace std;

using LL = long long;
int acnt[maxn], b[maxn], bcnt[maxn];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++)
    {
        int a;
        scanf("%d", &a);
        acnt[a] ++;
    }
    for(int i=0; i<n; i++)
        scanf("%d", b + i);
    for(int i=0; i<n; i++)
    {
        int c;
        scanf("%d", &c);
        bcnt[b[--c]] ++;
    }
    LL ans = 0LL;
    for(int i=1; i<=n; i++)
        ans += LL(acnt[i]) * LL(bcnt[i]);
    printf("%lld\n", ans);
    return 0;
}

D - aab aba baa

在由$A$个a和$B$个b（均不要求连续）组成的字符串中，求字典序第$K$小的。

$1\le A,B\le 30$
$1\le K\le S$（$S$为由$A$个a和$B$个b组成的字符串的个数）

输入格式

$A~B~K$

输出格式

输出由$A$个a和$B$个b组成的字符串中字典序第$K$小的。

样例

$A$	$B$	$K$	输出
$2$	$2$	$4$	`baab`
$30$	$30$	$118264581564861424$	（$30$个`b`$+30$个`a`)

分析

我们令$\mathrm{dp}(a,b)$为由$a$个a和$b$个b组成的字符串的个数，则：

我们在长度为$a+b-1$的字符串上再添上一个a或b：
$\mathrm{dp}(a,b)=\mathrm{dp}(a-1,b)+\mathrm{dp}(a,b-1)$。

$$f(a,b,k)=\begin{cases} ``" & (a=b=0)\\ ``a"+f(a-1,b,k) & (b=0)\\ ``b"+f(a,b-1,k) & (a=0)\\ ``a"+f(a-1,b,k) & (k\le \mathrm{dp}(a-1,b))\\ ``b"+f(a,b-1,k- \mathrm{dp}(a-1,b)) & (k>\mathrm{dp}(a-1,b)) \end{cases}$$

代码

写代码时，可以用递归形式，也可以使用非递归形式（更快）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


#include <cstdio>
#define maxn 35
using namespace std;

using LL = long long;
LL dp[maxn][maxn];

int main()
{
    int a, b;
    LL k;
    scanf("%d%d%lld", &a, &b, &k);
    for(int i=0; i<=a; i++) dp[i][0] = 1;
    for(int i=0; i<=b; i++) dp[0][i] = 1;
    for(int i=1; i<=a; i++)
        for(int j=1; j<=b; j++)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    while(a && b)
    {
        LL t = dp[a - 1][b];
        if(k <= t) putchar('a'), a --;
        else putchar('b'), b --, k -= t;
    }
    while(a--) putchar('a');
    while(b--) putchar('b');
    putchar('\n');
    return 0;
}

E - Count Descendants

我们有一棵$N$个节点的树，节点的编号分别为$1,2,\dots,N$。
$1$号点是根节点，且第$i$个点（$2\le i\le N$）的父亲节点是$P_i$。
给你$Q$个查询，第$i$个查询包含两个整数$U_i$和$D_i$，求符合下列条件的点$u$的个数：

$u$到根节点的最短路径正好有$D_i$条边；
$U_i$在$u$到根节点的最短路径中（包含两端）。

$1\le N\le 2\times10^5$
$1\le P_i < i$
$1\le Q\le 2\times10^5$
$1\le U_i\le N$
$0\le D_i < N$

输入格式

$N$
$P_2~P_3~\dots~P_N$
$Q$
$U_1~D_1$
$U_2~D_2$
$\vdots$
$U_Q~D_Q$

输出格式

输出$Q$行。第$i$行包含对第$i$个查询的回应。

样例

样例输入

1
2
3
4
5
6
7


7
1 1 2 2 4 2
4
1 2
7 2
4 1
5 5

样例输出

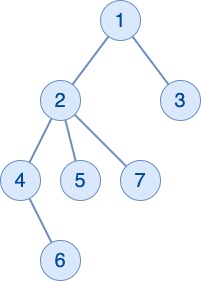
在第一个查询中，节点$4,5,7$符合条件。
在第二个查询中，只有节点$7$符合条件。
在最后两个查询中，没有节点符合条件。
样例说明

分析

我们可以先在整棵树上从根节点开始跑一遍$\text{DFS}$，对于节点$i$预处理出$\mathrm{in}_i$和$\mathrm{out}_i$，分别表示进入和走出这个节点的时间，同时将第$i$层节点的所有$\mathrm{in}$放入$\mathrm{depin}_i$。
如果节点$u$到根节点的路径中有$v$，则$\mathrm{in}_v\le\mathrm{in}_u < \mathrm{out}_v$。
因此，对于每个查询，我们利用二分查找即可快速算出符合条件的节点个数。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


#include <cstdio>
#include <vector>
#include <algorithm>
#define maxn 200005
using namespace std;

int in[maxn], out[maxn], dep[maxn], cnt;
vector<int> G[maxn], depin[maxn];

void dfs(int v)
{
    depin[dep[v]].push_back(in[v] = cnt++);
    for(int u: G[v])
        dfs(u);
    out[v] = cnt++;
}

int main()
{
    int n;
    scanf("%d", &n);
    dep[0] = cnt = 0;
    for(int i=1; i<n; i++)
    {
        int p;
        scanf("%d", &p);
        dep[i] = dep[--p] + 1;
        G[p].push_back(i);
    }
    dfs(0);
    int q;
    scanf("%d", &q);
    while(q--)
    {
        int u, d;
        scanf("%d%d", &u, &d);
        const auto& din = depin[d];
        auto first = lower_bound(din.begin(), din.end(), in[--u]);
        auto last = lower_bound(din.begin(), din.end(), out[u]);
        printf("%lld\n", last - first);
    }
    return 0;
}