A - Vanishing Pitch

题目大意

一个球的速度是$V~\text{m/s}$，它飞了$T$秒后会隐形，飞了$S$秒时会接触隐形。
球在飞了$D$米后，人能看见它吗？输出Yes或者No。

$1\le V\le 1000$
$1\le T < S\le 1000$
$1\le D\le 1000$

输入格式

$V~T~S~D$

输出格式

输出答案。

样例

$V$	$T$	$S$	$D$	输出
$10$	$3$	$5$	$20$	`Yes`
$10$	$3$	$5$	$30$	`No`

分析

如果$VT\le D\le VS$，则球飞了$D$米后是隐形的，人看不见，输出No；否则，输出Yes。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#include <cstdio>
using namespace std;

int main()
{
	int v, t, s, d;
	scanf("%d%d%d%d", &v, &t, &s, &d);
	puts((v * t <= d && d <= v * s)? "No": "Yes");
	return 0;
}

B - Remove It

题目大意

给你一个长度为$N$的整数序列$A$，请你将其中所有的$X$都删除并不改变顺序输出。

$1\le N\le 10^5$
$1\le X\le 10^9$
$1\le A_i\le 10^9$

输入格式

$N~X$
$A_1~A_2~\dots~A_N$

输出格式

输出最终序列，两个相邻的元素之间有一个空格。

样例

样例输入1

样例输出1

1

3 6 4

我们从序列$[3,5,6,5,4]$中删除所有的$5$，得到$[3,6,4]$。

样例输入2

样例输出2

当所有元素都被删除时，我们输出一个空行即可。

分析

这道题不需要真正删除所有的$X$，只需输出时不输出等于$X$的元素。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


#include <cstdio>
using namespace std;

int main()
{
	int n, x;
	scanf("%d%d", &n, &x);
	while(n--)
	{
		int a;
		scanf("%d", &a);
		if(a != x) printf("%d ", a);
	}
	putchar('\n');
	return 0;
}

C - Digital Graffiti

题目大意

我们有一张$H\times W$的方格纸，在$(i,j)$位置上的点是$S_{i,j}$。
每一个方格都是黑色（#）或白色（.），题目保证最外圈的点都是白色的。
黑色方格放在一起是一个多边形。求这个多边形的边数。

$3\le H,W\le 10$

输入格式

$H~W$
$S_{1,1}S_{1,2}\dots S_{1,W}$
$S_{2,1}S_{2,2}\dots S_{2,W}$
$\vdots$
$S_{H,1}S_{H,2}\dots S_{H,W}$

输出格式

输出答案。

样例

样例输入

1
2
3
4
5
6


5 5
.....
.###.
.###.
.###.
.....

样例输出

1

4

这是一个四边形。

自制数据

由于样例太简单，无法全面测试我们的程序。因此，博主再提供一组数据：

输入

1
2
3
4
5
6


5 5
.....
..#..
.###.
.#.#.
.....

输出

1

12

分析

很多人看到这种图就会想到$\text{DFS}$、$\text{BFS}$……其实这道题根本不需要。
这道题的做法来源于一个很简单的定理：多边形的顶点数=边数。
再进一步分析，一个点，在这个图上，怎样判断其是否为顶点？
其实，只要一个点周围四个方格中有一个或三个白方格，那么它就是一个顶点。
我们只要用一个$2\times 2$的正方形搜索即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


#include <cstdio>
#define maxn 15
using namespace std;

char c[maxn][maxn];

int main()
{
	int h, w, ans = 0;
	scanf("%d%d", &h, &w);
	for(int i=0; i<h; i++)
		scanf("%s", c[i]);
	for(int i=0; i<h-1; i++)
		for(int j=0; j<w-1; j++)
		{
			int cnt = 0;
			cnt += c[i][j] == '.';
			cnt += c[i][j + 1] == '.';
			cnt += c[i + 1][j] == '.';
			cnt += c[i + 1][j + 1] == '.';
			if(cnt == 1 || cnt == 3) ans ++;
		}
	printf("%d\n", ans);
	return 0;
}

D - Circle Lattice Points

题目大意

有一个中心为$(X,Y)$、半径为$R$的圆。
这个圆内（圆上的也算）有多少个栅格点（$X,Y$坐标均为整数的点）？

$|X| \le 10^5$
$|Y|\le 10^5$
$0\le R\le 10^5$
$X,Y,R$至多是四位小数。

输入格式

$X~Y~R$

输出格式

输出一行，即园内栅格点的个数。

样例

样例输入1

1

0.2 0.8 1.1

样例输出1

1

3

这个圆如下图所示。标了红色的是栅格点。
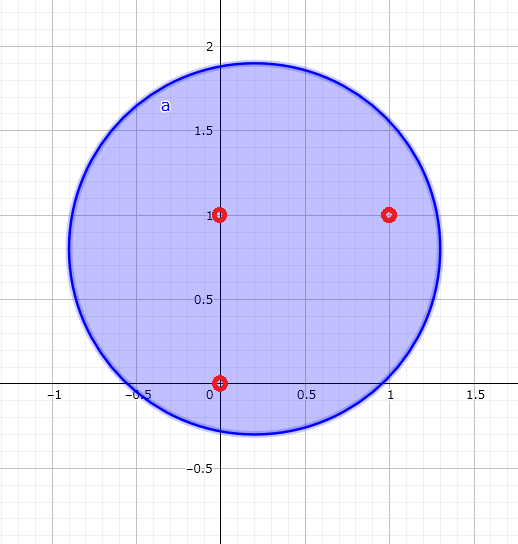
ABC191D示意图

样例输入2

1

100 100 1

样例输出2

1

5

$X,Y$和$R$也有可能是整数。
注意：正好在圆上的栅格点也计入总数内！

样例输入3

1

42782.4720 31949.0192 99999.99

样例输出3

1

31415920098

分析

$$(i-X)^2+(j-Y)^2=R^2$$$$(j-Y)^2=R^2-(i-X)^2$$$$j-Y=\sqrt{R^2-(i-X)^2}$$$$j=\sqrt{R^2-(i-X)^2}+Y$$$$j=\lfloor \sqrt {R^2-(i-X)^2}+Y\rfloor$$

对于任意一个$X$坐标，它的$Y_\text{up}$和$Y_\text{down}$是以圆心$Y$作为对称轴对称的，所以我们可以使用$2Y-Y_\text{up}$求得$Y_\text{down}$。
可惜的是，$\sqrt{R^2-(i-X)^2}$的计算结果可能有浮点数精度误差，我们的程序需要完全避开任何浮点数操作，所以这样做行不通。
其实，这道题可以二分。我们利用二分找到$X$坐标对应的最上面的点，再求出最下面的点和对应的栅格点即可。

代码

前面都是干货，下面上代码~
注意：long long不能忘！一定要判断各种负数的情况！

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78


#include <cstdio>
#define DIV 10000LL
using namespace std;

typedef long long LL;

LL x, y, R;

inline LL read()
{
	// Returns: input * 10000.
	LL res = 0LL;
	int num = 0;
	bool flag = false, negative = false;
	for(char c=getchar(); c != ' ' && c != '\n'; c=getchar())
	{
		if(c == '-') negative = true;
		else if(c == '.') flag = true;
		else
		{
			res *= 10LL;
			res += c - '0';
			if(flag) num ++;
		}
	}
	for(int i=num; i<4; i++)
		res *= 10LL;
	return negative? -res: res;
}

inline LL in_circle(const LL& dx, const LL& dy)
{
	return dx * dx + dy * dy <= R * R;
}

inline LL findtop(LL i)
{
	i *= DIV;
	LL l = y, r = y + R;
	while(l < r)
	{
		LL mid = l + r + 1LL >> 1LL;
		if(in_circle(i - x, mid - y))
			l = mid;
		else r = mid - 1LL;
	}
	return l;
}

inline LL ceildiv(const LL& a)
{
	// Returns: ceil(a / DIV).
	if(a < 0LL) return a / DIV;
	if(a % DIV == 0LL) return a / DIV;
	return a / DIV + 1LL;
}

inline LL floordiv(const LL& a)
{
	// Returns: floor(a / DIV).
	if(a >= 0LL) return a / DIV;
	if(a % DIV == 0LL) return a / DIV;
	return a / DIV - 1LL;
}

int main()
{
	x = read(), y = read(), R = read();
	LL ans = 0LL, left = ceildiv(x - R), right = floordiv(x + R);
	for(LL i=left; i<=right; i++)
	{
		LL top = findtop(i);
		LL bottom = (y << 1LL) - top;
		ans += floordiv(top) - ceildiv(bottom) + 1LL;
	}
	printf("%lld\n", ans);
	return 0;
}