题目大意
Takahashi要和Aoki见面。
他们计划在距离Takahashi家$D$米的地方$T$分钟后见面。
Takahashi将立即出门并以$S$米/分钟的速度朝见面地点走去。
Takahashi能按时到达吗?
$1\le D\le 10000$
$1\le T\le 10000$
$1\le S\le 10000$
输入格式
$D~T~S$
输出格式
如果Takahashi提前或准时到达此地,输出Yes;否则输出No。
样例
| D |
T |
S |
输出 |
| 1000 |
15 |
80 |
Yes |
| 2000 |
20 |
100 |
Yes |
| 10000 |
1 |
1 |
No |
分析
判断$\frac D S\le T$(简化后为 $TS\ge D$)即可。
代码
1
2
3
4
5
6
7
8
9
10
|
#include <cstdio>
using namespace std;
int main(int argc, char** argv)
{
int d, t, s;
scanf("%d%d%d", &d, &t, &s);
puts(t * s >= d? "Yes": "No");
return 0;
}
|
题目大意
给你两个字符串$S$和$T$。
请你修改$S$中的一些字符(可以不修改)使得$T$是$S$的字串。
至少需要修改多少个字符?
子串:如,xxx是yxxxy的子串,但不是xxyxx的子串。
$1\le |T|\le |S|\le 1000$
$S$和$T$都由小写英文字母组成。
输入格式
$S~T$
输出格式
一行,即至少需要修改的字符个数。
样例
样例输入1
样例输出1
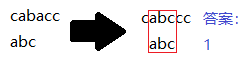
样例输入2
样例输出2

分析
我们只要将$T$在$S$中滚动匹配,寻找不同的字母数量的最小值即可。
代码
其实这就是枚举 :)
注意:如果按下面的代码写,最开始一定要特判$S$和$T$长度相等的情况!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include <cstdio>
#define maxn 1005
using namespace std;
char s[maxn], t[maxn];
int main(int argc, char** argv)
{
scanf("%s%s", s, t);
int tlen = 0, ans = maxn;
for(; t[tlen]; tlen++);
if(s[tlen] == '\0')
{
ans = 0;
for(int i=0; i<tlen; i++)
if(s[i] != t[i])
ans ++;
printf("%d\n", ans);
return 0;
}
for(int i=0; s[i+tlen]; i++)
{
int cnt = 0;
for(int j=0; j<tlen; j++)
if(s[i + j] != t[j])
cnt ++;
if(cnt < ans) ans = cnt;
}
printf("%d\n", ans);
return 0;
}
|
题目大意
给定$N$个整数$A_1,A_2,\dots,A_N$。
输出${\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^NA_iA_j} \mod {(10^9+7)}$,即符合$1\le i \lt j\le N$的所有$(i,j)$的$A_iA_j$的和,对$(10^9 + 7)$取模。
输入格式
$N$
$A_1~A_2~\dots~A_N$
输出格式
输出一行,即${\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^NA_iA_j} \mod {(10^9+7)}$。
样例
样例输入1
样例输出1
$1\times2+1\times3+2\times3=11$。
样例输入2
1
2
|
4
141421356 17320508 22360679 244949
|
样例输出2
不要忘记对$(10^9 + 7)$取模!
分析
我们需要将题目中的公式转化一下:
$${\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^NA_iA_j} \mod {(10^9+7)}$$
$${(\sum\limits_{i=2}^{N}\sum\limits_{j=0}^{i-1}A_iA_j)} \mod {(10^9+7)}$$
$${\sum\limits_{i=2}^{N}A_i(\sum\limits_{j=0}^{i-1}A_j)} \mod {(10^9+7)}$$
这时,我们只需循环遍历$i$,再设置一个变量记录$\sum\limits_{j=0}^{i-1}A_j$即可。
代码
可以输入时直接处理。
虽然要取模,但是还要使用long long:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <cstdio>
#define maxn 200005
#define MOD 1000000007LL
using namespace std;
typedef long long LL;
int main(int argc, char** argv)
{
int n;
LL sum, res = 0LL;
scanf("%d%lld", &n, &sum);
while(--n) // 循环 (n-1) 次
{
LL x;
scanf("%lld", &x);
res += sum * x;
sum += x;
res %= MOD, sum %= MOD;
}
printf("%lld\n", res);
return 0;
}
|
题目大意
有$N$个人,编号分别为$1$到$N$。
给你$M$个关系,第$i$个关系为“$A_i$号人和$B_i$号人是朋友。”(关系可能会重复给出)。
如果$X$和$Y$是朋友、$Y$和$Z$是朋友,则$X$和$Z$也是朋友。
Takahashi大坏蛋想把这$N$个人进行分组,使得每组中的人互不为朋友。他至少要分多少组?
$2\le N\le 2\times10^5$
$0\le M\le 2\times10^5$
$1\le A_i,B_i\le N$
$A_i \ne B_i$
输入格式
$N~M$
$A_1~B_1$
$A_2~B_2$
$\vdots$
$A_M~B_M$
输出格式
输出答案。
样例
样例输入1
样例输出1
分为三组:$\{1,3\}$、$\{2,4\}$、$\{5\}$可以达到目标。
样例输入2
1
2
3
4
5
6
7
8
9
10
11
|
4 10
1 2
2 1
1 2
2 1
1 2
1 3
1 4
2 3
2 4
3 4
|
样例输出2
请注意重复的关系。
样例输入3
1
2
3
4
5
|
10 4
3 1
4 1
5 9
2 6
|
样例输出3
分析
这道题可以先分出一个个朋友圈,再从朋友圈的人数中取最大值并输出即可。
代码
“分出朋友圈”这个操作可以使用dfs/bfs(不需要去重),当然,并查集也是可以的(需要去重)。我选择的是bfs。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
#include <cstdio>
#include <queue>
#include <vector>
#define maxn 200005
using namespace std;
vector<int> G[maxn];
bool vis[maxn];
int bfs(int x)
{
queue<int> q;
q.push(x);
int cnt = 0;
while(!q.empty())
{
x = q.front(); q.pop();
if(vis[x]) continue;
vis[x] = true, cnt ++;
for(int v: G[x])
q.push(v);
}
return cnt;
}
int main(int argc, char** argv)
{
int n, m;
scanf("%d%d", &n, &m);
for(int i=0; i<m; i++)
{
int x, y;
scanf("%d%d", &x, &y);
G[x].push_back(y);
G[y].push_back(x);
}
int ans = bfs(0);
for(int i=1; i<n; i++)
if(!vis[i])
{
int cnt = bfs(i);
if(cnt > ans)
ans = cnt;
}
printf("%d\n", ans);
return 0;
}
|

