这次比赛的题名很特殊,是由符号+(+英文+)组成的 :)
题目大意
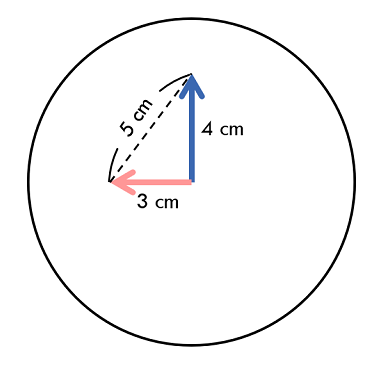
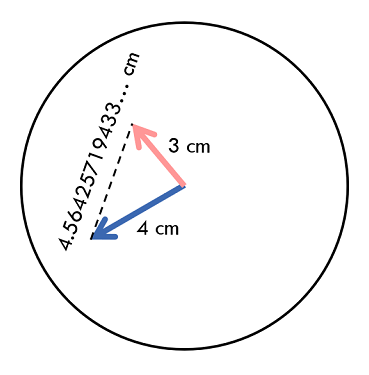
在$A$时$B$分,长度为$H$厘米的时针和长度为$M$厘米的分针的顶点的距离是多少?
$1\le A, B\le 1000$
$0\le H\le 11$
$0\le M\le 59$
(浮点数精度误差最多允许$10^{-9}$)
输入格式
$A~B~H~M$
输出格式
一行,即两点之间的距离。
样例
样例输入1
样例输出1
样例输入2
样例输出2
分析
其实是给定一个三角形,知道两条边和它们之间的夹角$\theta$(英文为theta),求另一条边的长度(设为C)。可以使用公式:
$$C^2=A^2+B^2-2AB\cos\theta$$
需要注意的是:C/C++中的cos函数的参数应是弧度,如$\theta$是角度请使用cos(theta / 180 * PI)
代码
终于上代码了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#include <cstdio>
#include <cmath>
#define PI 3.1415926535897932
using namespace std;
int main(int argc, char** argv)
{
int a, b, h, m;
scanf("%d%d%d%d", &a, &b, &h, &m);
int mangle = m * 6;
double hangle = h * 30 + m * 0.5;
double theta = abs(hangle - mangle);
if(theta > 180) theta = 360 - theta;
theta = theta / 180 * PI;
printf("%.13lf\n", sqrt(double(a * a + b * b) - 2.0 * a * b * cos(theta)));
return 0;
}
|
题目大意
有一个山洞,它有$N$个房间和$M$条通道。
房间的编号是$1$ ~ $N$,通道的编号是$1$ ~ $M$,每条通道双向连接$A_i$和$B_i$ ($1\le i\le M$)。房间$1$是山洞的出口。
现在要给每个房间标一个路标,指向一个和本房间被通道连接的房间。
每个房间(房间$1$除外)如果一直按照路标走向指示的房间,那么走的路径一定是最短的到出口的路径。
$2\le N\le 10^5$
$1\le M\le 2 * 10^5$
$1\le A_i, B_i\le N$ ($1\le i\le M$)
$A_i≠B_i$ ($1\le i\le M$)
输入格式
$N~M$
$A_1~B_1$
$\vdots$
$A_M~B_M$
输出格式
如果无解,输出No;
如果有解,第一行输出Yes,第$i$行输出房间$i$的路标指向的房间序号。($2\le i\le N$)
分析
明显bfs题目..
说明一点:如果给定山洞不连通,则无解。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <cstdio>
#include <vector>
#include <queue>
#define UNVISITED -1
#define maxn 100005
using namespace std;
typedef pair<int, int> pii;
vector<int> G[maxn];
int par[maxn];
int main(int argc, char** argv)
{
int n, m;
scanf("%d%d", &n, &m);
for(int i=0; i<n; i++) par[i] = UNVISITED;
for(int i=0; i<m; i++)
{
int x, y;
scanf("%d%d", &x, &y);
G[--x].push_back(--y);
G[y].push_back(x);
}
queue<pii> q;
q.push(pii(0, -1));
while(!q.empty())
{
int room = q.front().first, p = q.front().second;
q.pop();
if(par[room] != UNVISITED) continue;
par[room] = p;
for(int i=0; i<G[room].size(); i++)
q.push(pii(G[room][i], room));
}
for(int i=1; i<n; i++)
if(par[i] == UNVISITED)
{
puts("No");
return 0;
}
puts("Yes");
for(int i=1; i<n; i++) printf("%d\n", par[i] + 1);
return 0;
}
|

