【Algorithm Notes】Multi-source Shortest Path Problem—

Translation Notice
This article was machine-translated using DeepSeek-R1.

Original Version: Authored in Chinese by myself

Accuracy Advisory: Potential discrepancies may exist between translations

Precedence: The Chinese text shall prevail in case of ambiguity

Feedback: Technical suggestions regarding translation quality are welcomed

Preface

In graphs, when requiring distances between any two points, we can use Floyd ($\mathcal O(N^3)$;)）and Dijkstra ($\mathcal O(NM\log M)$:)). For relatively small data ranges (typically vertex count $N\le 150$), Floyd’s algorithm is suitable. This article explains the principles, implementation, and extended applications of Floyd’s algorithm.

If there are any shortcomings, please feel free to provide feedback. Thank you!

Principle

$$ f(x,y)= \begin{cases} 0 & (x=y) \\ G[x][y] & (G[x][y]\ne0)\\ +\infty & (x\ne y,G[x][y]=0) \end{cases} $$

where $G$ is the adjacency matrix of the graph, $G[x][y]$ represents the edge weight from vertex $x$ to $y$, and $0$ indicates no edge between $x$ and $y$.
Next, consider enumerating intermediate points $k$ and calculating the shortest path via the route $x\to k\to y$. The pseudocode is:

1
2
3
4


for k = 1, 2, ..., n
    for x = 1, 2, ..., n
        for y = 1, 2, ..., n
            f[x][y] = min(f[x][y], f[x][k] + f[k][y])

At this point, the algorithm concludes, and the final $f(x,y)$ represents the shortest path from $x$ to $y$.

Note: When the given graph is undirected, for any $(x,y)$, $G[x][y]=G[y][x]$, so $f(x,y)=f(y,x)$. The computation process can be adjusted (e.g., using f[k][x]+f[k][y]). However, for directed graphs, strictly follow the order in the pseudocode!

Code

The code for Floyd’s algorithm can be submitted on Luogu B3647. Below is the AC code for this problem (note edge-based input):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


#include <cstdio>
#include <cstring>
#define maxn 100
using namespace std;

int dis[maxn][maxn];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    // Initialize, note that initial values should not exceed INT_MAX/2 (to prevent overflow from adding two INFs)
    memset(dis, 0x3f, sizeof dis); 
    // Distance from each point to itself is 0
    for(int i=0; i<n; i++)
        dis[i][i] = 0;
    // Read edges
    while(m--)
    {
        int u, v, d;
        scanf("%d%d%d", &u, &v, &d);
        u --, v --; // 0-index
        dis[u][v] = dis[v][u] = d; // Note both values need to be set
    }
    // Floyd algorithm process
    for(int k=0; k<n; k++) // Intermediate point
        for(int i=0; i<n; i++) // Start point
            for(int j=0; j<n; j++) // End point
            {
                int d = dis[i][k] + dis[k][j]; // i->k->j
                if(d < dis[i][j]) dis[i][j] = d; // Take shortest length
            }
    for(int i=0; i<n; i++, putchar('\n'))
        for(int j=0; j<n; j++)
            printf("%d ", dis[i][j]);
    return 0;
}

Extension

Now the question arises: How to output the result path? The method is simple. Similar to Dijkstra but slightly different, let $\text{path}(x, y)$ be a point on the shortest path from $x\to y$. When updating $f(x,y)$ during state transition if $f(x,k)+f(k,y) < f(x,y)$, not only update $f(x,y)$ but also set $\text{path}(x,y):=k$. Finally, recursively output the result.

Problem Statement

Given a simple undirected graph with $N$ vertices and $M$ edges, for every pair $(i,j)$ ($1\le i < j\le N$), output every vertex on the shortest path from $i\to j$.

Sample

Input:

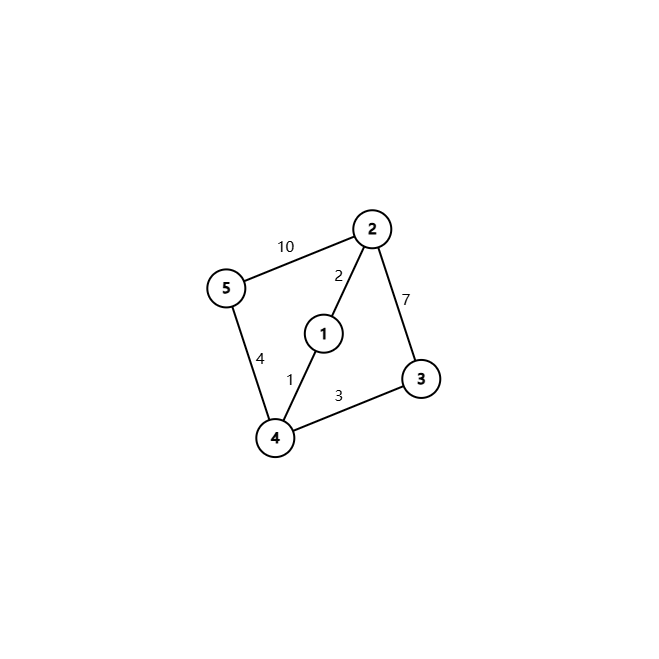
Input Image

Output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


1->2: 1 2
1->3: 1 4 3
1->4: 1 4
1->5: 1 4 5
2->3: 2 1 4 3
2->4: 2 1 4
2->5: 2 1 4 5
3->4: 3 4
3->5: 3 4 5
4->5: 4 5

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


#include <cstdio>
#include <cstring>
#define maxn 100
using namespace std;

int dis[maxn][maxn], path[maxn][maxn];
void print(int x, int y) // Recursively output path x->y, excluding y
{
    int k = path[x][y]; // x->k->y
    if(k == x || k == y) // Adjacent vertices, output directly
        printf(" %d", x);
    else
    {
        // Split into two recursive parts
        print(x, k); // x->k
        print(k, y); // k->y
    }
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    // Initialize
    memset(dis, 0x3f, sizeof dis); 
    for(int i=0; i<n; i++)
        dis[i][i] = 0;
    // Read edges
    while(m--)
    {
        int u, v, d;
        scanf("%d%d%d", &u, &v, &d);
        dis[u][v] = dis[v][u] = d; // Note both values need to be set
        path[u][v] = path[v][u] = u; // Initialize path
    }
    // Floyd algorithm process, using 1-index for easier output
    for(int k=1; k<=n; k++) // Intermediate point
        for(int i=1; i<=n; i++) // Start point
            for(int j=1; j<=n; j++) // End point
            {
                int d = dis[i][k] + dis[k][j]; // i->k->j
                if(d < dis[i][j]) // Update shortest path
                    dis[i][j] = d, path[i][j] = k;
            }
    // Enumerate (i,j) and output paths
    for(int i=1; i<n; i++)
        for(int j=i+1; j<=n; j++)
        {
            printf("%d->%d:", i, j);
            print(i, j);
            printf(" %d\n", j);
        }
    return 0;
}

Note: Since the length of each path won’t exceed $N$, the overall time complexity remains $\mathcal O(N^3)$.

Epilogue

Summary: Floyd’s algorithm has a time complexity of $\mathcal O(N^3)$ and is convenient to implement. If you found this helpful, please give a like/share/follow—thank you for your support!