Translation Notice
This article was machine-translated using DeepSeek-R1.

• Original Version: Authored in Chinese by myself
• Accuracy Advisory: Potential discrepancies may exist between translations
• Precedence: The Chinese text shall prevail in case of ambiguity
• Feedback: Technical suggestions regarding translation quality are welcomed

C - Knight Fork

Problem Statement

Determine if there exists an integer coordinate point on the 2D plane whose Euclidean distances to both $(x_1,y_1)$ and $(x_2,y_2)$ are $\sqrt{5}$.

Input Format

$x_1~y_1~x_2~y_2$

Output Format

Print Yes if such a point exists; otherwise, print No.

Sample Cases

Analysis

Thus, for the point $(0,0)$, the points with distance $\sqrt{5}$ are shown below (similar for other points):

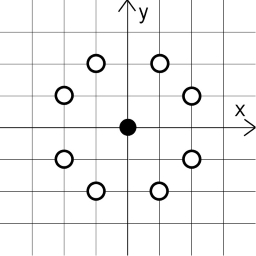
We generate all points with distance $\sqrt{5}$ from $(x_1,y_1)$ and check their distances to $(x_2,y_2)$.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include <cstdio>
using namespace std;

using LL = long long;
const int d[8] = {-1, 1, 2, 2, 1, -1, -2, -2};

inline LL sqr2(const LL& x, const LL& y)
{
    return x * x + y * y;
}

int main()
{
    LL x1, y1, x2, y2;
    scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2);
    x1 -= x2, y1 -= y2;
    for(int i=0; i<8; i++)
        if(sqr2(x1 + d[i], y1 + d[(i + 2) & 7]) == 5)
        {
            puts("Yes");
            return 0;
        }
    puts("No");
    return 0;
}

D - Prime Sum Game

==Water problem warning==

Problem Statement

Takahashi and Aoki play a game as follows:

1. Takahashi selects an integer $A\le N\le B$.
2. Aoki selects an integer $C\le M\le D$.
3. If $N+M$ is prime, Aoki wins. Otherwise, Takahashi wins.

Determine the winner when both play optimally.

$1\le A\le B\le 100$
$1\le C\le D\le 100$

Input Format

$A~B~C~D$

Output Format

Print the winner’s name: Takahashi or Aoki.

Sample Cases

Analysis

The key is understanding “optimal play”:

• Takahashi wins if there exists an $N$ such that $N+M$ is never prime for any $M$.
• Aoki wins if for every $N$, there exists an $M$ making $N+M$ prime.

Given small constraints, we brute-force all pairs. Time complexity is $\mathcal O(BD)$.

Code

P.S. Surprisingly, runtime is 4ms (expected ~30ms).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <cstdio>
using namespace std;

inline bool isprime(int x)
{
    for(int t=__builtin_sqrt(x), i=2; i<=t; i++)
        if(x % i == 0)
            return false;
    return true;
}

int main()
{
    int a, b, c, d;
    scanf("%d%d%d%d", &a, &b, &c, &d);
    for(int i=a; i<=b; i++)
    {
        int j = c;
        for(; j<=d; j++)
            if(isprime(i + j))
                break;
        if(j > d) { puts("Takahashi"); return 0; }
    }
    puts("Aoki");
    return 0;
}

E - Subtree K-th Max

Problem Statement

Given a tree with $N$ nodes (1-based) rooted at node 1. Each node $v$ has a value $X_v$.
Answer $Q$ queries $(V_i,K_i)$:

• Find the K-th largest value (without deduplication) in the subtree rooted at $V_i$.

$2\le N,Q\le 10^5$
$0\le X_i\le 10^9$
$1\le A_i,B_i,V_i\le N$
==$1\le K_i\le 20$==

Input Format

$N~Q$
$X_1~\dots~X_N$
$A_1~B_1$
$\vdots$
$A_{N-1}~B_{N-1}$
$V_1~K_1$
$\vdots$
$V_Q~K_Q$

Output Format

Print $Q$ lines. The i-th line contains the answer to the i-th query.

Sample Cases

See AtCoder for details.

Analysis

Given $1\le K\le 20$, precompute the top-20 values for each node’s subtree. Use DFS to merge node values and children’s top-20 lists. Sorting can be optimized with priority_queue. Time complexity is $\mathcal O(N+Q)$.

Code

Sample implementation uses DFS with priority_queue (190ms runtime):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

#include <cstdio>
#include <queue>
#define maxn 100005
using namespace std;

int x[maxn];
vector<int> G[maxn], dp[maxn];

void dfs(int v, int par)
{
    priority_queue<int, vector<int>, greater<int>> q;
    q.push(x[v]);
    for(int u: G[v])
        if(u != par)
        {
            dfs(u, v);
            for(int val: dp[u])
            {
                q.push(val);
                if(q.size() > 20) q.pop();
            }
        }
    while(!q.empty())
    {
        dp[v].push_back(q.top());
        q.pop();
    }
}

int main()
{
    int n, q;
    scanf("%d%d", &n, &q);
    for(int i=0; i<n; i++)
        scanf("%d", x + i);
    for(int i=1; i<n; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        G[--a].push_back(--b);
        G[b].push_back(a);
    }
    dfs(0, -1);
    while(q--)
    {
        int v, k;
        scanf("%d%d", &v, &k);
        const auto& d = dp[--v];
        printf("%d\n", d[d.size() - k]);
    }
    return 0;
}