Translation Notice
This article was machine-translated using DeepSeek-R1.

Original Version: Authored in Chinese by myself

Accuracy Advisory: Potential discrepancies may exist between translations

Precedence: The Chinese text shall prevail in case of ambiguity

Feedback: Technical suggestions regarding translation quality are welcomed

A - Three Dice

A person rolled three dice with top faces showing $a$, $b$, and $c$. Find the sum of their bottom faces.
The dice used are standard, meaning the sum of opposite faces is $7$.

$1\le a,b,c\le 6$

Input Format

$a~b~c$

Output Format

Print the answer.

Samples

$a$	$b$	$c$	Answer
$1$	$4$	$3$	$13$
$5$	$6$	$4$	$6$

Analysis

Since opposite faces sum to $7$, the answer is $(7-a)+(7-b)+(7-c)=21-a-b-c$.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#include <cstdio>
using namespace std;

int main()
{
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    printf("%d\n", 21 - a - b - c);
    return 0;
}

B - 180°

Given a string $S$ consisting of 0, 1, 6, 8, 9. Rotate it 180° and output the result.

How to rotate a string 180°:

Reverse the string.

Replace 6 with 9 and 9 with 6.

$1\le |S|\le10^5$

Input Format

$S$

Output Format

Print the rotated string.

Samples

$S$	Output
`0601889`	`6881090`
`86910`	`01698`
`01010`	`01010`

Analysis

Directly simulate the rotation process.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


#include <cstdio>
#define maxn 100005
using namespace std;

char s[maxn];

int main()
{
    int n = 0;
    char c;
    while((c = getchar()) != '\n')
        s[n++] = c;
    while(n--)
        putchar(s[n] == '6'? '9': s[n] == '9'? '6': s[n]);
    putchar('\n');
    return 0;
}

C - Made Up

Given three sequences $A$, $B$, $C$ of length $N$. Count the number of pairs $(i,j)$ satisfying $A_i=B_{C_j}$.

$1\le N\le 10^5$
$1\le A_i,B_i,C_i\le N$

Input Format

$N$
$A_1~A_2~\dots~A_N$
$B_1~B_2~\dots~B_N$
$C_1~C_2~\dots~C_N$

Output Format

Print the count.

Samples

Sample Input 1

Sample Output 1

1

4

Valid pairs: $(1,1),(1,3),(2,2),(3,2)$.

Sample Input 2

Sample Output 2

1

16

All pairs are valid.

Sample Input 3

Sample Output 3

1

0

No valid pairs.

Analysis

An $O(n^2)$ brute-force approach would TLE. Instead, count frequencies using bucket arrays $\mathrm{acnt}$ and $\mathrm{bcnt}$, then compute the sum $\sum_{i=1}^n\mathrm{acnt}_i\mathrm{bcnt}_i$.

Code

Note: Use long long to avoid overflow!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


#include <cstdio>
#define maxn 100005
using namespace std;

using LL = long long;
int acnt[maxn], b[maxn], bcnt[maxn];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++)
    {
        int a;
        scanf("%d", &a);
        acnt[a] ++;
    }
    for(int i=0; i<n; i++)
        scanf("%d", b + i);
    for(int i=0; i<n; i++)
    {
        int c;
        scanf("%d", &c);
        bcnt[b[--c]] ++;
    }
    LL ans = 0LL;
    for(int i=1; i<=n; i++)
        ans += LL(acnt[i]) * LL(bcnt[i]);
    printf("%lld\n", ans);
    return 0;
}

D - aab aba baa

Find the $K$-th lexicographically smallest string consisting of $A$ as and $B b`s.

$1\le A,B\le30$
$1\le K\le S$ ($S$ is the total number of valid strings)

Input Format

$A~B~K$

Output Format

Print the required string.

Samples

$A$	$B$	$K$	Output
$2$	$2$	$4$	`baab`
$30$	$30$	$118264581564861424$	(30 `b`s + 30 `a`s)

Analysis

Let $\mathrm{dp}(a,b)$ be the count of strings with $a$ as and $b` `b`s. The recursive formula is: $\mathrm{dp}(a,b)=\mathrm{dp}(a-1,b)+\mathrm{dp}(a,b-1)$. Construct the string greedily by comparing $K$ with $\mathrm{dp}(a-1,b)$ at each step.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


#include <cstdio>
#define maxn 35
using namespace std;

using LL = long long;
LL dp[maxn][maxn];

int main()
{
    int a, b;
    LL k;
    scanf("%d%d%lld", &a, &b, &k);
    for(int i=0; i<=a; i++) dp[i][0] = 1;
    for(int i=0; i<=b; i++) dp[0][i] = 1;
    for(int i=1; i<=a; i++)
        for(int j=1; j<=b; j++)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    while(a && b)
    {
        LL t = dp[a - 1][b];
        if(k <= t) putchar('a'), a --;
        else putchar('b'), b --, k -= t;
    }
    while(a--) putchar('a');
    while(b--) putchar('b');
    putchar('\n');
    return 0;
}

E - Count Descendants

Given an $N$-node tree rooted at node 1. The parent of node $i$ ($2\le i\le N$) is $P_i$. Answer $Q$ queries: count nodes $u$ where:

The path from $u$ to root has exactly $D_i$ edges.
$U_i$ lies on this path (including endpoints).

$1\le N\le 2\times10^5$
$1\le P_i $1\le Q\le 2\times10^5$
$1\le U_i\le N$
$0\le D_i < N$

Input Format

$N$
$P_2~P_3~\dots~P_N$
$Q$
$U_1~D_1$
$U_2~D_2$
$\vdots$
$U_Q~D_Q$

Output Format

Print $Q$ lines, each containing the answer.

Samples

Sample Input

1
2
3
4
5
6
7


7
1 1 2 2 4 2
4
1 2
7 2
4 1
5 5

Sample Output

Explanation:

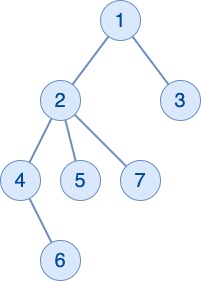
Query 1: Nodes 4,5,7.
Query 2: Node 7.
Queries 3-4: No valid nodes.

Analysis

Preprocess each node’s entry/exit timestamps via DFS. For each depth $d$, collect all entry times. For a query $(U_i,D_i)$, count nodes at depth $D_i$ whose entry time is between $U_i$’s entry and exit times using binary search.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


#include <cstdio>
#include <vector>
#include <algorithm>
#define maxn 200005
using namespace std;

int in[maxn], out[maxn], dep[maxn], cnt;
vector<int> G[maxn], depin[maxn];

void dfs(int v)
{
    depin[dep[v]].push_back(in[v] = cnt++);
    for(int u: G[v])
        dfs(u);
    out[v] = cnt++;
}

int main()
{
    int n;
    scanf("%d", &n);
    dep[0] = cnt = 0;
    for(int i=1; i<n; i++)
    {
        int p;
        scanf("%d", &p);
        dep[i] = dep[--p] + 1;
        G[p].push_back(i);
    }
    dfs(0);
    int q;
    scanf("%d", &q);
    while(q--)
    {
        int u, d;
        scanf("%d%d", &u, &d);
        const auto& din = depin[d];
        auto first = lower_bound(din.begin(), din.end(), in[--u]);
        auto last = lower_bound(din.begin(), din.end(), out[u]);
        printf("%lld\n", last - first);
    }
    return 0;
}