Translation Notice
This article was machine-translated using DeepSeek-R1.

Original Version: Authored in Chinese by myself

Accuracy Advisory: Potential discrepancies may exist between translations

Precedence: The Chinese text shall prevail in case of ambiguity

Feedback: Technical suggestions regarding translation quality are welcomed

A - Vanishing Pitch

Problem Summary

A ball travels at $V~\text{m/s}$. It becomes invisible after flying for $T$ seconds and remains invisible after $S$ seconds. Can the person see the ball after it has flown $D$ meters? Output Yes or No.

Constraints:
$1\le V\le 1000$
$1\le T < S\le 1000$
$1\le D\le 1000$

Input Format

V T S D

Output Format

Output the answer.

Samples

$V$	$T$	$S$	$D$	Output
$10$	$3$	$5$	$20$	`Yes`
$10$	$3$	$5$	$30$	`No`

Analysis

If $VT \le D \le VS$, the ball is invisible after flying $D$ meters (output No); otherwise, output Yes.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#include <cstdio>
using namespace std;

int main()
{
    int v, t, s, d;
    scanf("%d%d%d%d", &v, &t, &s, &d);
    puts((v * t <= d && d <= v * s)? "No": "Yes");
    return 0;
}

B - Remove It

Problem Summary

Given an integer sequence $A$ of length $N$, remove all occurrences of $X$ and output the remaining elements in their original order.

Constraints:
$1\le N\le 10^5$
$1\le X\le 10^9$
$1\le A_i\le 10^9$

Input Format

Line 1: N X
Line 2: A_1 A_2 ... A_N

Output Format

Output the filtered sequence with elements separated by spaces.

Samples

Sample Input 1

Sample Output 1

1

3 6 4

After removing all 5s from [3,5,6,5,4], we get [3,6,4].

Sample Input 2

Sample Output 2

Output a blank line when all elements are removed.

Analysis

The problem does not require actual deletion of all $X$ elements; simply skip outputting elements equal to $X$ during printing.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


#include <cstdio>
using namespace std;

int main()
{
    int n, x;
    scanf("%d%d", &n, &x);
    while(n--)
    {
        int a;
        scanf("%d", &a);
        if(a != x) printf("%d ", a);
    }
    putchar('\n');
    return 0;
}

C - Digital Graffiti

Problem Summary

Given a $H \times W$ grid where each cell is black (#) or white (.). The outermost cells are guaranteed to be white. The black cells form a polygon. Find the number of edges of this polygon.

Constraints:
$3\le H,W\le 10$

Input Format

Line 1: H W
Lines 2~H+1: Grid rows.

Output Format

Print the number of edges.

Sample

Sample Input

1
2
3
4
5
6


5 5
.....
.###.
.###.
.###.
.....

Sample Output

1

4

The shape is a quadrilateral.

Custom Test Case

Input

1
2
3
4
5
6


5 5
.....
..#..
.###.
.#.#.
.....

Output

1

12

Analysis

The number of vertices of a polygon equals its number of edges. A cell is a vertex if among its four adjacent cells, exactly one or three are white. Count such vertices by checking all $2 \times 2$ squares.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


#include <cstdio>
#define maxn 15
using namespace std;

char c[maxn][maxn];

int main()
{
    int h, w, ans = 0;
    scanf("%d%d", &h, &w);
    for(int i=0; i<h; i++)
        scanf("%s", c[i]);
    for(int i=0; i<h-1; i++)
        for(int j=0; j<w-1; j++)
        {
            int cnt = 0;
            cnt += c[i][j] == '.';
            cnt += c[i][j + 1] == '.';
            cnt += c[i + 1][j] == '.';
            cnt += c[i + 1][j + 1] == '.';
            if(cnt == 1 || cnt == 3) ans ++;
        }
    printf("%d\n", ans);
    return 0;
}

D - Circle Lattice Points

Problem Summary

Count the number of lattice points (integer coordinates) inside or on a circle with center $(X,Y)$ and radius $R$.

Constraints:
$|X|, |Y| \le 10^5$
$0 \le R \le 10^5$
$X, Y, R$ may have up to 4 decimal places.

Input Format

X Y R

Output Format

Print the total count.

Samples

Sample Input 1

1

0.2 0.8 1.1

Sample Output 1

1

3

The red marks in the figure indicate valid lattice points.
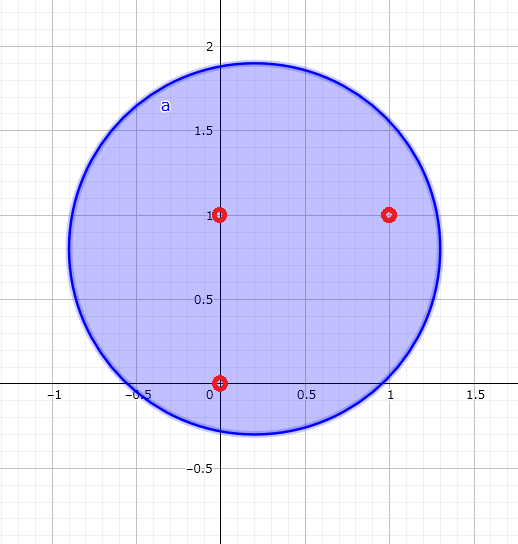
ABC191D Illustration

Sample Input 2

1

100 100 1

Sample Output 2

1

5

Note: Points exactly on the circle are counted.

Sample Input 3

1

42782.4720 31949.0192 99999.99

Sample Output 3

1

31415920098

Analysis

Precision handling: Multiply all values by $10^4$ to avoid floating-point errors. For each integer $x$ coordinate within the circle’s horizontal range, use binary search to find the maximum and minimum $y$ coordinates and count valid lattice points.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78


#include <cstdio>
#define DIV 10000LL
using namespace std;

typedef long long LL;

LL x, y, R;

inline LL read()
{
    // Returns: input * 10000.
    LL res = 0LL;
    int num = 0;
    bool flag = false, negative = false;
    for(char c=getchar(); c != ' ' && c != '\n'; c=getchar())
    {
        if(c == '-') negative = true;
        else if(c == '.') flag = true;
        else
        {
            res *= 10LL;
            res += c - '0';
            if(flag) num ++;
        }
    }
    for(int i=num; i<4; i++)
        res *= 10LL;
    return negative? -res: res;
}

inline LL in_circle(const LL& dx, const LL& dy)
{
    return dx * dx + dy * dy <= R * R;
}

inline LL findtop(LL i)
{
    i *= DIV;
    LL l = y, r = y + R;
    while(l < r)
    {
        LL mid = l + r + 1LL >> 1LL;
        if(in_circle(i - x, mid - y))
            l = mid;
        else r = mid - 1LL;
    }
    return l;
}

inline LL ceildiv(const LL& a)
{
    // Returns: ceil(a / DIV).
    if(a < 0LL) return a / DIV;
    if(a % DIV == 0LL) return a / DIV;
    return a / DIV + 1LL;
}

inline LL floordiv(const LL& a)
{
    // Returns: floor(a / DIV).
    if(a >= 0LL) return a / DIV;
    if(a % DIV == 0LL) return a / DIV;
    return a / DIV - 1LL;
}

int main()
{
    x = read(), y = read(), R = read();
    LL ans = 0LL, left = ceildiv(x - R), right = floordiv(x + R);
    for(LL i=left; i<=right; i++)
    {
        LL top = findtop(i);
        LL bottom = (y << 1LL) - top;
        ans += floordiv(top) - ceildiv(bottom) + 1LL;
    }
    printf("%lld\n", ans);
    return 0;
}