AtCoder Beginner Contest 188 A~D Solutions

Translation Notice
This article was machine-translated using DeepSeek-R1.

  • Original Version: Authored in Chinese by myself
  • Accuracy Advisory: Potential discrepancies may exist between translations
  • Precedence: The Chinese text shall prevail in case of ambiguity
  • Feedback: Technical suggestions regarding translation quality are welcomed

A - Three-Point Shot

Problem Statement

Two teams have scores of $X$ and $Y$ points respectively. Determine if the team with fewer points can overtake the other after gaining three points.

$0\le X,Y\le 100$
$X \ne Y$
$X$ and $Y$ are integers.

Input Format

$X~Y$

Output Format

Print Yes if possible; otherwise, print No.

Sample

X Y Output
3 5 Yes

Analysis

This is straightforward: check if the difference between the two numbers is less than 3.

Code 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

#include <cstdio>
#include <algorithm>
using namespace std;

int main(int argc, char** argv)
{
    int a, b;
    scanf("%d%d", &a, &b);
    puts((abs(a - b) < 3)? "Yes": "No");
    return 0;
}

B - Orthogonality

Problem Statement

Given two arrays $A=\{A_1,A_2,...,A_N\}$ and $B=\{B_1,B_2,...,B_N\}$ of length $N$, determine if their dot product is zero. In other words, check if $\sum\limits_{i=1}^NA_iB_i = 0$.

$1\le N\le 10^5$
$-100\le A_i,B_i\le 100$ Note: Negative values may appear!

Input Format

$N$
$A_1~A_2~...~A_N$
$B_1~B_2~...~B_N$

Output Format

Print Yes if the dot product is zero; otherwise, print No.

Samples

Sample Input 1 

1
2
3

2
-3 6
4 2

Sample Output 1 

1

Yes

$N = 2$
$A = \{-3,6\}$
$B = \{4,2\}$
Dot product: $(-3)\times4 + 6\times2 = 0$, so output Yes.

Sample Input 2 

1
2
3

2
4 5
-1 -3

Sample Output 2 

1

No

$N = 2$
$A = \{4,5\}$
$B = \{-1,-3\}$
Dot product: $4\times(-1) + 5\times(-3) = -19$, so output No.

Sample Input 3 

1
2
3

3
1 3 5
3 -6 3

Sample Output 3 

1

Yes

$N = 3$
$A = \{1,3,5\}$
$B = \{3,-6,3\}$
Dot product: $1\times3 + 3\times(-6) + 5\times3 = 0$, so output Yes.

Analysis

Compute the dot product directly as described.

Code 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <cstdio>
#define maxn 100005
using namespace std;

int a[maxn];

int main(int argc, char** argv)
{
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++)
        scanf("%d", a + i);
    int res = 0;
    for(int i=0; i<n; i++)
    {
        int x;
        scanf("%d", &x);
        res += x * a[i];
    }
    puts(res == 0? "Yes": "No");
    return 0;
}

C - ABC Tournament

Problem Statement

There are $2^N$ players, each with a unique rank $A_i$. The tournament consists of $N$ knockout rounds. Determine the index of the runner-up (the player eliminated in the final round).

$1\le N\le 16$
$1\le A_i \le 10^9$
All $A_i$ are distinct.

Input Format

$N$
$A_1~A_2~...~A_{2^N}$

Output Format

Print the index of the runner-up.

Samples

Sample Input 1 

1
2

2
1 4 2 5

Sample Output 1 

1

2

Players: 1,4,2,5
Round 1: 1 vs 4 (4 wins), 2 vs 5 (5 wins)
Round 2: 4 vs 5 (5 wins). Runner-up: 2 (eliminated in round 2).

Sample Input 2 

1
2

2
3 1 5 4

Sample Output 2 

1

1

Players: 3,1,5,4
Round 1: 3 vs 1 (3 wins), 5 vs 4 (5 wins)
Round 2: 3 vs 5 (5 wins). Runner-up: 1 (eliminated in round 2).

Sample Input 3 

1
2

4
6 13 12 5 3 7 10 11 16 9 8 15 2 1 14 4

Sample Output 3 

1

2

Blogger’s note: Manual calculation shows that simply sorting and selecting the second-highest value is incorrect!

Analysis

Simulate the tournament using a queue. Track pairs of (rank, index) and compare adjacent pairs in each round. The final two elements determine the runner-up.

Code

Notes:

  1. Use long long for ranks.
  2. Use pair to track indices.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <cstdio>
#include <queue>
using namespace std;

using LL = long long;
using pli = pair<LL, int>;

int main(int argc, char** argv)
{
    queue<pli> q;
    int n;
    scanf("%d", &n);
    n = 1 << n;
    for(int i=1; i<=n; i++)
    {
        LL x;
        scanf("%lld", &x);
        q.emplace(x, i);
    }
    while(q.size() > 2)
    {
        pli x = q.front(); q.pop();
        pli y = q.front(); q.pop();
        if(x < y) q.push(y);
        else q.push(x);
    }
    pli x = q.front(); q.pop();
    pli y = q.front();
    printf("%d\n", x < y? x.second: y.second);
    return 0;
}

D - Snuke Prime

Problem Statement

Takahashi uses $N$ services. Each service $i$ costs $c_i$ yuan per day, active from day $a_i$ to $b_i$ inclusive. Alternatively, a subscription service costs $C$ yuan per day, granting unlimited access. Determine the minimum total cost.

$1\le N\le 2\times 10^5$
$1\le C\le 10^9$
$1\le a_i\le b_i\le 10^9$
$1\le c_i\le 10^9$

Input Format

$N~C$
$a_1~b_1~c_1$
$a_2~b_2~c_2$
$...$
$a_N~b_N~c_N$

Output Format

Print the minimum total cost.

Samples

Sample Input 1 

1
2
3

2 6
1 2 4
2 2 4

Sample Output 1 

1

10

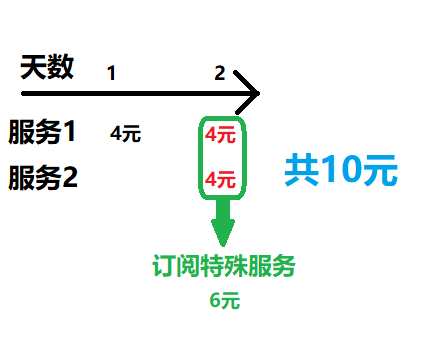
sample1_note

Sample Input 2 

1
2
3
4
5
6

5 1000000000
583563238 820642330 44577
136809000 653199778 90962
54601291 785892285 50554
5797762 453599267 65697
468677897 916692569 87409

Sample Output 2 

1

163089627821228

Optimal solution: Do not use the subscription.

Sample Input 3 

1
2
3
4
5
6

5 100000
583563238 820642330 44577
136809000 653199778 90962
54601291 785892285 50554
5797762 453599267 65697
468677897 916692569 87409

Sample Output 3 

1

88206004785464

Custom Sample

Input:

1
2
3

2 7
1 3 5
2 6 4

Output:

1

31

Subscribe on days 2 and 3.

Analysis

Split each service into two events: $(a_i-1, +c_i)$ and $(b_i, -c_i)$. Sort events by time. Track the daily cost (fee) and compute the minimum cost for each interval between events using min(C, fee).

Code

Notes:

  • Use long long for all variables.
  • Use pair to store events.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pll;

int main(int argc, char** argv)
{
    int n;
    LL c;
    scanf("%d%lld", &n, &c);
    priority_queue<pll, vector<pll>, greater<pll> > q;
    while(n--)
    {
        LL x, y, z;
        scanf("%lld%lld%lld", &x, &y, &z);
        q.emplace(--x, z);
        q.emplace(y, -z);
    }
    LL ans = 0LL, fee = 0LL, last = 0LL;
    while(!q.empty())
    {
        auto [day, cost] = q.top(); q.pop();
        if(last != day)
        {
            ans += min(c, fee) * (day - last);
            last = day;
        }
        fee += cost;
    }
    printf("%lld\n", ans);
    return 0;
}

Alternative code for compatibility:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pll;

int main(int argc, char** argv)
{
    int n;
    LL c;
    scanf("%d%lld", &n, &c);
    priority_queue<pll, vector<pll>, greater<pll> > q;
    while(n--)
    {
        LL x, y, z;
        scanf("%lld%lld%lld", &x, &y, &z);
        q.push(pll(--x, z));
        q.push(pll(y, -z));
    }
    LL ans = 0LL, fee = 0LL, last = 0LL;
    while(!q.empty())
    {
        LL day = q.top().first, cost = q.top().second; q.pop();
        if(last != day)
        {
            ans += min(c, fee) * (day - last);
            last = day;
        }
        fee += cost;
    }
    printf("%lld\n", ans);
    return 0;
}
© 2020 - 2025 GoodCoder's Blog
Built with Hugo
Theme Stack designed by Jimmy