Translation Notice
This article was machine-translated using DeepSeek-R1.

• Original Version: Authored in Chinese by myself
• Accuracy Advisory: Potential discrepancies may exist between translations
• Precedence: The Chinese text shall prevail in case of ambiguity
• Feedback: Technical suggestions regarding translation quality are welcomed

A - Don’t be late

Problem Statement

Takahashi plans to meet Aoki.
They will meet at a location $D$ meters away from Takahashi’s house in $T$ minutes.
Takahashi will leave immediately and walk towards the meeting point at a speed of $S$ meters per minute.
Can Takahashi arrive on time?

$1\le D\le 10000$
$1\le T\le 10000$
$1\le S\le 10000$

Input Format

$D~T~S$

Output Format

Print Yes if Takahashi arrives on time or early; otherwise print No.

Samples

Analysis

Check whether $\frac D S\le T$ (simplified as $TS\ge D$).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

#include <cstdio>
using namespace std;

int main(int argc, char** argv)
{
    int d, t, s;
    scanf("%d%d%d", &d, &t, &s);
    puts(t * s >= d? "Yes": "No");
    return 0;
}

B - Substring

Problem Statement

Given two strings $S$ and $T$.
Modify some characters in $S$ (possibly none) to make $T$ a substring of $S$.
What is the minimum number of characters to modify?
Substring: e.g., xxx is a substring of yxxxy but not of xxyxx.

$1\le |T|\le |S|\le 1000$
$S$ and $T$ consist of lowercase English letters.

Input Format

$S~T$

Output Format

Print the minimum number of characters to modify.

Samples

Sample Input1

1
2

cabacc
abc

Sample Output1

1

1

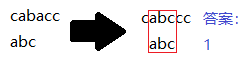
Sample Input2

1
2

codeforces
atcoder

Sample Output2

1

6

Analysis

Slide $T$ over $S$ and find the position with the minimum number of differing characters.

Code

This is essentially brute force enumeration :)
Note: If following the code below, ensure to handle the case where $S$ and $T$ have equal lengths first!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <cstdio>
#define maxn 1005
using namespace std;

char s[maxn], t[maxn];

int main(int argc, char** argv)
{
    scanf("%s%s", s, t);
    int tlen = 0, ans = maxn;
    for(; t[tlen]; tlen++);
    if(s[tlen] == '\0')
    {
        ans = 0;
        for(int i=0; i<tlen; i++)
            if(s[i] != t[i])
                ans ++;
        printf("%d\n", ans);
        return 0;
    }
    for(int i=0; s[i+tlen]; i++)
    {
        int cnt = 0;
        for(int j=0; j<tlen; j++)
            if(s[i + j] != t[j])
                cnt ++;
        if(cnt < ans) ans = cnt;
    }
    printf("%d\n", ans);
    return 0;
}

C - Sum of product of pairs

Problem Statement

Given $N$ integers $A_1,A_2,\dots,A_N$.
Compute ${\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^NA_iA_j} \mod {(10^9+7)}$, i.e., the sum of products of all pairs $(i,j)$ where $1\le i \lt j\le N$, modulo $(10^9 + 7)$.

Input Format

$N$
$A_1~A_2~\dots~A_N$

Output Format

Print the result.

Samples

Sample Input1

1
2

3
1 2 3

Sample Output1

1

11

$1\times2+1\times3+2\times3=11$.

Sample Input2

1
2

4
141421356 17320508 22360679 244949

Sample Output2

1

437235829

Don’t forget to take modulo $(10^9 + 7)$!

Analysis

Maintain a cumulative sum while iterating through the array.

Code

Process input incrementally.
Use long long despite modulo operations:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <cstdio>
#define maxn 200005
#define MOD 1000000007LL
using namespace std;

typedef long long LL;

int main(int argc, char** argv)
{
    int n;
    LL sum, res = 0LL;
    scanf("%d%lld", &n, &sum);
    while(--n) // Loop (n-1) times
    {
        LL x;
        scanf("%lld", &x);
        res += sum * x;
        sum += x;
        res %= MOD, sum %= MOD;
    }
    printf("%lld\n", res);
    return 0;
}

D - Friends

Problem Statement

There are $N$ people numbered $1$ to $N$.
Given $M$ relationships, where the $i$-th states “Person $A_i$ and $B_i$ are friends.” (may contain duplicates).
If $X$ and $Y$ are friends, and $Y$ and $Z$ are friends, then $X$ and $Z$ are friends.
Takahashi wants to divide these people into groups where no two people in the same group are friends. What is the minimum number of groups required?

$2\le N\le 2\times10^5$
$0\le M\le 2\times10^5$
$1\le A_i,B_i\le N$
$A_i \ne B_i$

Input Format

$N~M$
$A_1~B_1$
$A_2~B_2$
$\vdots$
$A_M~B_M$

Output Format

Print the answer.

Samples

Sample Input1

1
2
3
4

5 3
1 2
3 4
5 1

Sample Output1

1

3

Three groups: $\{1,3\}$, $\{2,4\}$, $\{5\}$.

Sample Input2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

4 10
1 2
2 1
1 2
2 1
1 2
1 3
1 4
2 3
2 4
3 4

Sample Output2

1

4

Note duplicate relationships.

Sample Input3

1
2
3
4
5

10 4
3 1
4 1
5 9
2 6

Sample Output3

1

3

Analysis

Find all connected components (friend circles) and output the size of the largest component.

Code

Use BFS/DFS or Union-Find to find connected components. Here BFS is implemented.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include <cstdio>
#include <queue>
#include <vector>
#define maxn 200005
using namespace std;

vector<int> G[maxn];
bool vis[maxn];

int bfs(int x)
{
    queue<int> q;
    q.push(x);
    int cnt = 0;
    while(!q.empty())
    {
        x = q.front(); q.pop();
        if(vis[x]) continue;
        vis[x] = true, cnt ++;
        for(int v: G[x])
            q.push(v);
    }
    return cnt;
}

int main(int argc, char** argv)
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i=0; i<m; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    int ans = bfs(0);
    for(int i=1; i<n; i++)
        if(!vis[i])
        {
            int cnt = bfs(i);
            if(cnt > ans)
                ans = cnt;
        }
    printf("%d\n", ans);
    return 0;
}