Translation Notice
This article was machine-translated using DeepSeek-R1.

Original Version: Authored in Chinese by myself

Accuracy Advisory: Potential discrepancies may exist between translations

Precedence: The Chinese text shall prevail in case of ambiguity

Feedback: Technical suggestions regarding translation quality are welcomed

The problem titles in this contest are unique, composed of symbols + (+English+) :)

C - : (Colon)

Problem Statement

At $A$ hours and $B$ minutes, what is the distance between the tips of the hour hand of length $H$ centimeters and the minute hand of length $M$ centimeters?
$1\le A, B\le 1000$
$0\le H\le 11$
$0\le M\le 59$
(Floating-point precision errors up to $10^{-9}$ are allowed)

Input Format

$A~B~H~M$

Output Format

A single line with the distance between the two points.

Samples

Sample Input 1

1

3 4 9 0

Sample Output 1

1

5.00000000000000000000

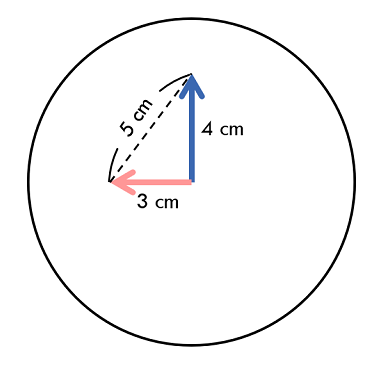
Distance 5cm

Sample Input 2

1

3 4 10 40

Sample Output 2

1

4.56425719433005567605

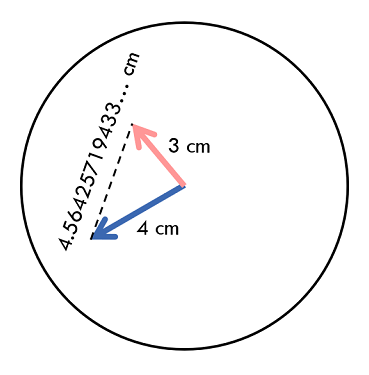
Approximate distance 4.56425cm

Analysis

$$C^2=A^2+B^2-2AB\cos\theta$$

Note: In C/C++, the parameter of the cos function is in radians. If θ is in degrees, use cos(theta / 180 * PI).

Code

Finally, the code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


#include <cstdio>  
#include <cmath>  
#define PI 3.1415926535897932  
using namespace std;  

int main(int argc, char** argv)  
{  
    int a, b, h, m;  
    scanf("%d%d%d%d", &a, &b, &h, &m);  
    int mangle = m * 6;  
    double hangle = h * 30 + m * 0.5;  
    double theta  = abs(hangle - mangle);  
    if(theta > 180) theta = 360 - theta;  
    theta = theta / 180 * PI;  
    printf("%.13lf\n", sqrt(double(a * a + b * b) - 2.0 * a * b * cos(theta)));  
    return 0;  
}  

D - . . (Double Dots)

Problem Statement

A cave has $N$ rooms and $M$ passages.
Rooms are numbered $1$ to $N$, passages are numbered $1$ to $M$. Each passage bidirectionally connects rooms $A_i$ and $B_i$ ($1\le i\le M$). Room $1$ is the exit.

Each room (except room $1$) must have a sign pointing to an adjacent room. Following these signs from any room must yield the shortest path to the exit.
$2\le N\le 10^5$
$1\le M\le 2 \times 10^5$
$1\le A_i, B_i\le N$ ($1\le i\le M$)
$A_i≠B_i$ ($1\le i\le M$)

Input Format

$N~M$
$A_1~B_1$
$\vdots$
$A_M~B_M$

Output Format

If no solution exists, output No.
If a solution exists:

First line: Yes
Line $i$: The room number pointed by the sign in room $i$ ($2\le i\le N$).

Analysis

Clearly a BFS problem. Note: If the cave is disconnected, there is no solution.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45


#include <cstdio>  
#include <vector>  
#include <queue>  
#define UNVISITED -1  
#define maxn 100005  
using namespace std;  

typedef pair<int, int> pii;  

vector<int> G[maxn];  
int par[maxn];  

int main(int argc, char** argv)  
{  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<n; i++) par[i] = UNVISITED;  
    for(int i=0; i<m; i++)  
    {  
        int x, y;  
        scanf("%d%d", &x, &y);  
        G[--x].push_back(--y);  
        G[y].push_back(x);  
    }  
    queue<pii> q;  
    q.push(pii(0, -1));  
    while(!q.empty())  
    {  
        int room = q.front().first, p = q.front().second;  
        q.pop();  
        if(par[room] != UNVISITED) continue;  
        par[room] = p;  
        for(int i=0; i<G[room].size(); i++)  
            q.push(pii(G[room][i], room));  
    }  
    for(int i=1; i<n; i++)  
        if(par[i] == UNVISITED)  
        {  
            puts("No");  
            return 0;  
        }  
    puts("Yes");  
    for(int i=1; i<n; i++) printf("%d\n", par[i] + 1);  
    return 0;  
}  